B .
B .  C .
C .  D .
D . 
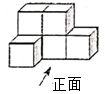
 B .
B .  C .
C . 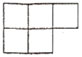 D .
D . 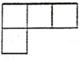
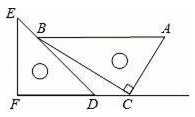
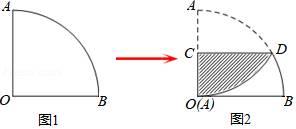
上述结论中正确的个数是( )

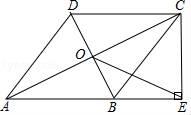
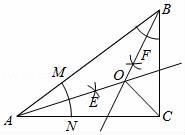
①以A为圆心,任意长为半径作弧,分别交AB、AC于点M、N;②分别以点M、N为圆心,以大于 MN的长为半径作弧,两弧相交于点E;③作射线AE;④以同样的方法作射线BF,AE交BF于点O,连接OC,则OC=
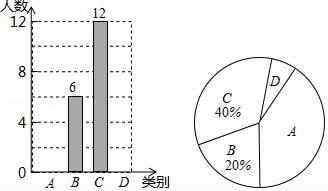
请依据统计结果回答下列问题:
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 ▲ 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?