 B .
B .  C .
C .  D .
D . 
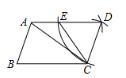
第一步,以点A为圆心,BC长为半径作弧.再以点C为圆心,AB长为半径作弧,两弧的交点记为D,连结AD,CD;
第二步,以点D为圆心,CD长为半径作弧,交AD于点E,连结CE.则∠BCE的度数为( )

|
编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
得分(分) |
3 |
4 |
3 |
5 |
5 |
4 |
3 |
5 |
5 |
4 |

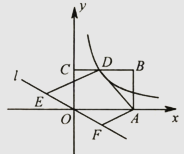
请根据以上不完整的统计图提供的信息,解答下列问题:


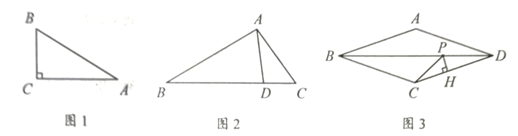
求BC的长.
求证:△ABD是倍比三角形,并求出倍比;
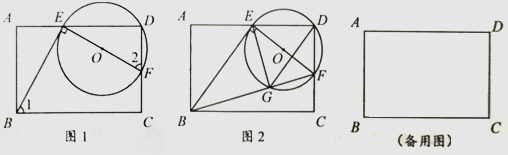
①用含t的代数式表示DF的长;
②连结DG.若△EGD是以EG为腰的等腰三角形。求t的值.