2016-2017学年江苏省无锡市江阴市青阳片九年级下学期期...

更新时间：2017-05-26 浏览次数：992 类型：期中考试

一、选择题

1. 如果a与﹣3互为相反数，则a等于（）

A . $\text{[math]}$ B . 3 C . ﹣ $\text{[math]}$ D . ﹣3

答案解析收藏纠错 + 选题
2. (2017·宜兴模拟) 下列各式运算中，正确的是（）

A . （a+b）²=a²+b² B . $\text{[math]}$ C . a³•a⁴=a¹² D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 下列调查方式中适合的是（）

A . 要了解一批节能灯的使用寿命，采用普查方式 B . 调查你所在班级同学的身高，采用抽样调查方式 C . 环保部门调查沱江某段水域的水质情况，采用抽样调查方式 D . 调查全市中学生每天的就寝时间，采用普查方式

答案解析收藏纠错 + 选题
4. (2017·薛城模拟) 图中所示几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. 如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（）

A . ∠1=∠3 B . ∠2+∠3=180° C . ∠2+∠4＜180° D . ∠3+∠5=180°

答案解析收藏纠错 + 选题
6. 关于抛物线y=（x﹣1）²+2，下列结论中不正确是（）

A . 对称轴为直线x=1 B . 当x＜1时，y随x的增大而减小 C . 与x轴没有交点 D . 与y轴交于点（0，2）

答案解析收藏纠错 + 选题
7. 晓明家到学校的路程是3500米，晓明每天早上7：30离家步行去上学，在8：10（含8：10）至8：20（含8：20）之间到达学校．如果设晓明步行的速度为x米/分，则晓明步行的速度范围是（）

A . 70≤x≤87.5 B . x≤70或x≥87.5 C . x≤70 D . x≥87.5

答案解析收藏纠错 + 选题
8. 如图，已知菱形OABC的顶点O（0，0），B（﹣2，﹣2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）

A . （1，﹣1） B . （﹣1，﹣1） C . （1，1） D . （﹣1，1）

答案解析收藏纠错 + 选题
9. (2017·宁波模拟) 当m，n是实数且满足m﹣n=mn时，就称点Q（m， $\text{[math]}$ ）为“奇异点”，已知点A、点B是“奇异点”且都在反比例函数y= $\text{[math]}$ 的图象上，点O是平面直角坐标系原点，则△OAB的面积为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2017·宁波模拟) 分解因式：a²﹣4a+4=．

答案解析收藏纠错 + 选题
11. (2017九下·东台开学考) 据媒体报道，我国因环境污染造成的巨大经济损失，每年高达680000000元，这个数用科学记数法表示为元．

答案解析收藏纠错 + 选题
12. 若一个多边形的内角和比外角和大360°，则这个多边形的边数为．

答案解析收藏纠错 + 选题
13. 一组数据1，2，a，4，5的平均数是3，则这组数据的方差为．

答案解析收藏纠错 + 选题
14. 有一个正六面体，六个面上分别写有1～6这6个整数，投掷这个正六面体一次，向上一面的数字是2的倍数或3的倍数的概率是．

答案解析收藏纠错 + 选题
15. 如图，△ABC中，DE∥FG∥BC，AD：DF：FB=2：3：4，若EG=4，则AC=．

答案解析收藏纠错 + 选题
16. 如图，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y= $\text{[math]}$ 的图象上，则k的值为．

答案解析收藏纠错 + 选题
17. 如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是．

答案解析收藏纠错 + 选题

三、解答题

18. 计算：
1. （1）（﹣3）²﹣ $\text{[math]}$ +（ $\text{[math]}$ ）^﹣¹ ．
2. （2）（x+1）²﹣2（x﹣2）．
答案解析收藏纠错 + 选题
19. 计算。
1. （1）解方程： $\text{[math]}$ +3= $\text{[math]}$
2. （2）解不等式：2x﹣3≤ $\text{[math]}$ （x+2）
答案解析收藏纠错 + 选题
20. 如图，C是线段AB的中点，CD=BE，CD∥BE．求证：∠D=∠E．

答案解析收藏纠错 + 选题
21. 中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
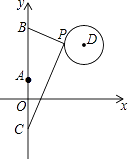
成绩x/分
频数
频率
50≤x＜60
10
0.05
　60≤x＜70
30
0.15
　70≤x＜80
40
n
　80≤x＜90
m
0.35
　90≤x≤100
50
0.25
请根据所给信息，解答下列问题：
1. （1） m=，n=；
2. （2）请补全频数分布直方图；
3. （3）这次比赛成绩的中位数会落在分数段；
4. （4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
答案解析收藏纠错 + 选题
22. 本校有A、B两个餐厅，甲、乙两名学生各自随机选择其中一个餐厅用餐，请用列表或画树状图的方法解答：
1. （1）甲、乙两名学生在同一餐厅用餐的概率；
2. （2）甲、乙两名学生至少有一人在B餐厅的概率．
答案解析收藏纠错 + 选题

23. 2008年5月12日四川汶川地区发生8.0级特大地震．举国上下通过各种方式表达爱心．某企业决定用p万元援助灾区n所学校，用于搭建帐篷和添置教学设备．根据各校不同的受灾情况，该企业捐款的分配方案是：所有学校得到的捐款数都相等，到第n所学校时捐款恰好分完，捐款的分配方法如下表所示．（其中p，n，a都是正整数）根据以上信息，解答下列问题：

（1）写出p与n的关系式；
（2）当p=125时，该企业能援助多少所学校？

（3）根据震区灾情，该企业计划再次提供不超过20a万元的捐款，按照原来的分配方案援助其它学校．若a由（2）确定，则再次提供的捐款最多又可以援助多少所学校？

分配顺序	分配数额（单位：万元）
分配顺序	帐篷费用	教学设备费用
第1所学校	5	剩余款的 $\text{[math]}$
第2所学校	10	再剩余款的 $\text{[math]}$
第3所学校	15	再剩余款的 $\text{[math]}$
…	…	…
第（n﹣1）所学校	5（n﹣1）	再剩余款的 $\text{[math]}$
第n所学校	5n	0

答案解析收藏纠错 + 选题

24. 在正方形网格中以点A为圆心，AB为半径作圆A交网格于点C（如图（1）），过点C作圆的切线交网格于点D，以点A为圆心，AD为半径作圆交网格于点E（如图（2））．
问题：
1. （1）求∠ABC的度数；
2. （2）求证：△AEB≌△ADC；
3. （3） △AEB可以看作是由△ADC经过怎样的变换得到的？并判断△AED的形状（不用说明理由）．
4. （4）如图（3），已知直线a，b，c，且a∥b，b∥c，在图中用直尺、三角板、圆规画等边三角形A′B′C′，使三个顶点A′，B′，C′，分别在直线a，b，c上．要求写出简要的画图过程，不需要说明理由．
答案解析收藏纠错 + 选题
25.
如图，已知二次函数y=ax²﹣2ax+c（a＜0）的图象与x轴负半轴交于点A（﹣1，0），与y轴正半轴交于点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．
1. （1）求一次函数解析式；
2. （2）求顶点P的坐标；
3. （3）平移直线AB使其过点P，如果点M在平移后的直线上，且 $\text{[math]}$ ，求点M坐标；
4. （4）设抛物线的对称轴交x轴于点E，连接AP交y轴于点D，若点Q、N分别为两线段PE、PD上的动点，连接QD、QN，请直接写出QD+QN的最小值．
答案解析收藏纠错 + 选题
26. 阅读图1的情景对话，然后解答问题：
1. （1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是命题（填“真”或“假”）
2. （2）在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；
3. （3）如图2，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆 $\text{[math]}$ 的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．
  ①求证：△ACE是奇异三角形；
  ②当△ACE是直角三角形时，求∠AOC的度数．
答案解析收藏纠错 + 选题
27.
如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．
1. （1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度；
2. （2）在（1）的条件下，小红想用△EFG包裹矩形ABCD，她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红．
答案解析收藏纠错 + 选题