湖北省2019届高三理数4月份调研考试试卷

更新时间：2021-05-20 浏览次数：553 类型：高考模拟

一、单选题

1. (2019·湖北模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020高二下·莆田期中) 已知复数 $\text{[math]}$ ，则下列关系式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019·湖北模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019·湖北模拟) 已知双曲线 $\text{[math]}$ $\text{[math]}$ 的离心率为 $\text{[math]}$ ，则双曲线 $\text{[math]}$ 的渐近线方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·湖北模拟) 如图，网格纸上的小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·湖北模拟) 已知函数 $\text{[math]}$ 是定义域为 $\text{[math]}$ 的奇函数，当 $\text{[math]}$ 时， $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019·湖北模拟) 甲乙2人从4门课程中各自选修2门课程，并且所选课程中恰有1门课程相同，则不同的选法方式有（）

A . 36种 B . 30种 C . 24种 D . 12种

答案解析收藏纠错 + 选题
8. (2019·湖北模拟) 如图，圆 $\text{[math]}$ 是边长为 $\text{[math]}$ 的等边三角形 $\text{[math]}$ 的内切圆，其与 $\text{[math]}$ 边相切于点 $\text{[math]}$ ，点 $\text{[math]}$ 为圆上任意一点， $\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·湖北模拟) 在 $\text{[math]}$ 中，给出下列说法：
①若 $\text{[math]}$ ，则一定有 $\text{[math]}$ ；②恒有 $\text{[math]}$ ；③若 $\text{[math]}$ ，则 $\text{[math]}$ 为锐角三角形.其中正确说法的个数有（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
10. (2019·湖北模拟) 已知函数 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 恒成立，且 $\text{[math]}$ 在区间 $\text{[math]}$ 上恰有两个零点，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019高三上·新疆月考) 生活中人们常用“通五经贯六艺”形容一个人才识技艺过人，这里的“六艺”其实源于中国周朝的贵族教育体系，具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化，某校在周末学生业余兴趣活动中开展了“六艺”知识讲座，每艺安排一节，连排六节，则满足“数”必须排在前两节，“礼”和“乐”必须分开安排的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019·湖北模拟) 已知不等式 $\text{[math]}$ （ $\text{[math]}$ ，且 $\text{[math]}$ ）对任意实数 $\text{[math]}$ 恒成立，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2019高二下·九台期中) 在 $\text{[math]}$ 的展开式中 $\text{[math]}$ 的系数为.

答案解析收藏纠错 + 选题
14. (2019·湖北模拟) 已知实数 $\text{[math]}$ ， $\text{[math]}$ 满足约束条件 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题
15. (2019·湖北模拟) 已知正三棱锥 $\text{[math]}$ 的底面边长为3，外接球的表面积为 $\text{[math]}$ ，则正三棱锥 $\text{[math]}$ 的体积为.

答案解析收藏纠错 + 选题
16. (2019·湖北模拟) 如图，过抛物线 $\text{[math]}$ $\text{[math]}$ 的焦点 $\text{[math]}$ 作两条互相垂直的弦 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 面积之和的最小值为16，则抛物线的方程为.

答案解析收藏纠错 + 选题

三、解答题

17. (2019高二上·河南月考) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ，其前 $\text{[math]}$ 项和为 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等差数列.
1. （1）求证 $\text{[math]}$ 为等差数列；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2019·湖北模拟) 已知四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 底面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 变化时，点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离是否为定值？若是，请求出该定值；若不是，请说明理由；
2. （2）当直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成的角为45°时，求二面角 $\text{[math]}$ 的余弦值.
答案解析收藏纠错 + 选题
19. (2019·湖北模拟) 已知椭圆 $\text{[math]}$ $\text{[math]}$ 的离心率为 $\text{[math]}$ ，椭圆上的点到左焦点的最小值为 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 的方程；
2. （2）已知直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，点 $\text{[math]}$ 为直线 $\text{[math]}$ 上任意一点，设直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的斜率分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则是否存在实数 $\text{[math]}$ ，使得 $\text{[math]}$ 恒成立？若是，请求出 $\text{[math]}$ 的值；若不是，请说明理由.
答案解析收藏纠错 + 选题
20. (2019·湖北模拟) 近年来，随着网络的普及，数码产品早已走进千家万户的生活，为了节约资源，促进资源循环利用，折旧产品回收行业得到迅猛发展，电脑使用时间越长，回收价值越低，某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计，得到如图所示的频率分布直方图，在如图对时间使用的分组中，将使用时间落入各组的频率视为概率.
1. （1）若在该市场随机选取3个2018年成交的二手电脑，求至少有2个使用时间在 $\text{[math]}$ 上的概率；
2. （2）根据电脑交易市场往年的数据，得到如图所示的散点图，其中 $\text{[math]}$ （单位：年）表示折旧电脑的使用时间， $\text{[math]}$ （单位：百元）表示相应的折旧电脑的平均交易价格.
  
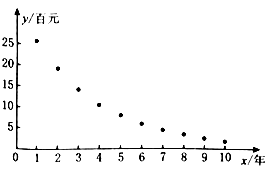
  （ⅰ）由散点图判断，可采用 $\text{[math]}$ 作为该交易市场折旧电脑平均交易价格与使用年限 $\text{[math]}$ 的回归方程，若 $\text{[math]}$ ， $\text{[math]}$ ，选用如下参考数据，求 $\text{[math]}$ 关于 $\text{[math]}$ 的回归方程.
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  5.5
  
  8.5
  
  1.9
  
  301.4
  
  79.75
  
  385
  
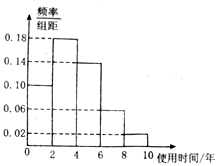
  （ⅱ）根据回归方程和相关数据，并用各时间组的区间中点值代表该组的值，估算该交易市场收购1000台折旧电脑所需的费用
  
  附：参考公式：对于一组数据 $\text{[math]}$ ，其回归直线 $\text{[math]}$ 的斜率和截距的最小二乘估计分别为： $\text{[math]}$ ， $\text{[math]}$ .参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2019·湖北模拟) 已知 $\text{[math]}$ $\text{[math]}$ .
1. （1）若 $\text{[math]}$ 是 $\text{[math]}$ 上的增函数，求 $\text{[math]}$ 的取值范围；
2. （2）若函数 $\text{[math]}$ 有两个极值点，判断函数 $\text{[math]}$ 零点的个数.
答案解析收藏纠错 + 选题
22. (2019·湖北模拟) 在直角坐标系 $\text{[math]}$ 中，曲线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 是参数），以坐标原点 $\text{[math]}$ 为极点， $\text{[math]}$ 轴的正半轴为极轴建立极坐标系，曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ .
1. （1）求曲线 $\text{[math]}$ 的极坐标方程和曲线 $\text{[math]}$ 的直角坐标方程；
2. （2）若射线 $\text{[math]}$ $\text{[math]}$ 与曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，求 $\text{[math]}$ 取最大值时 $\text{[math]}$ 的值
答案解析收藏纠错 + 选题
23. (2019·湖北模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，解不等式 $\text{[math]}$ ；
2. （2）若不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ，正数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值
答案解析收藏纠错 + 选题