一、选择题:本题共12小题,每小题5分,共60分。
-
A . {-1,0,1}
B . {0,1}
C . {-1,1}
D . {0,1,2}
-
A . -1-i
B . -1+i
C . 1-i
D . 1+i
-
3.
(2019·全国Ⅲ卷文)
《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并成为中国古典小说四大名著。某中学为了了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A . 0.5
B . 0.6
C . 0.7
D . 0.8
-
A . 12
B . 16
C . 20
D . 24
-
-
A . a=e,b=-1
B . a=e,b=1
C . a=e-1 , b=1
D . a=e-1 , b=-1
-
-
8.
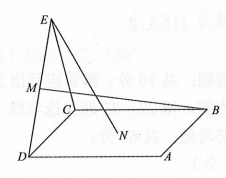
如图,点
N为正方形
ABCD的中心,△
ECD为正三角形,平面
ECD⊥平面
ABCD ,
M是线段
ED的中点,则( )
A . BM=EN , 且直线BM、EN 是相交直线
B . BM≠EN , 且直线BM , EN 是相交直线
C . BM=EN , 且直线BM、EN 是异面直线
D . BM≠EN , 且直线BM , EN 是异面直线
-
-
10.
(2021高二上·肇东月考)
双曲线

的右焦点为F,点P 在C的一条渐近线上,O为坐标原点,若|PO|=|PF|,则△PFO的面积为( )
-
A .  (log3
(log3  )>
)>  (
(  )>
)>  (
(  )
B .
)
B .  (log3
(log3  )>
)>  (
(  )>
)>  (
(  )
C .
)
C .  (
(  )>
)>  (
(  )>
)>  (log3
(log3  )
D .
)
D .  (
(  )>
)>  (
(  )>
)>  (log3
(log3  )
)
-
12.
(2019·全国Ⅲ卷理)
设函数f(x)=sin(ωx+

)(ω>0),已如f(x)在[0,2π]有且仅有5个零点,下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在(0,

)单调递增④ω的取值范围[

,

)其中所有正确结论的编号是( )
A . ①④
B . ②③
C . ①②③
D . ①③④
二、填空题:本题共4小题,每小题5分,共20分.
-
-
-
15.
(2020高二上·榆树期末)
设F
1 , F
2为椭圆C:

的两个焦点,M为C上一点且在第一象限,若△MF
1F
2为等腰三角形,则M的坐标为
。
-
16.
(2019·全国Ⅲ卷文)
学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为长方体ABCD-A
1B
1C
1D
1 , 挖去四棱推O一EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA
1=4cm,3D打印所用原料密度为0.9g/cm
2 , 不考虑打印损耗,制作该模型所需原料的质量为
g.

三、解答题,共70分,第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答:
-
17.
(2020高二上·贵港期中)
为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
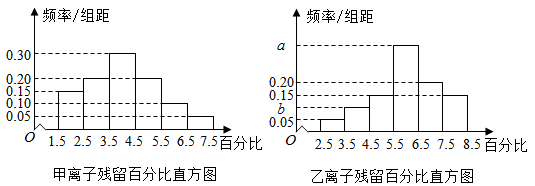
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
-
-
(2)
分别估计甲,乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表)
-
-
-
(2)
若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
-
19.
(2019·全国Ⅲ卷理)
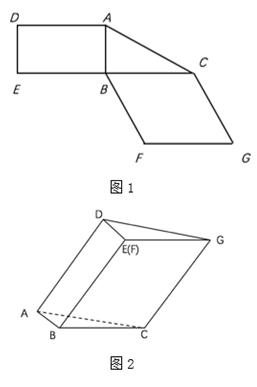
图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.
-
(1)
证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
-
-
-
-
(2)
是否存在a,b,使得f(x)在区间[0,1]的最小值为-1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由。
-
-
-
(2)
若以E(0,

)为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
四、选考题:共10分,请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
-
-
(1)
分别写出M1 , M2 , M3的极坐标方程;
-
(2)
曲线由M
1 , M
2 , M
3构成,若点P在M上,且|OP|=

,求P的极坐标。
-
-
(1)
求(x-1)2+(y+1)2+(z-1)2的最小值;
-
(2)
若(x-2)
2+(y-1)
2+(z-2)
2≥

成立,证明:a≤-3或a≥-1。
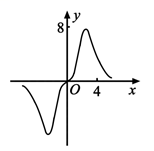 B .
B . 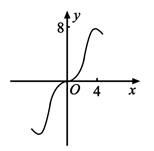 C .
C . 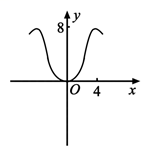 D .
D . 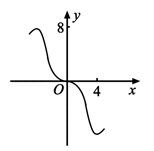



,
),C(
,
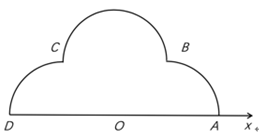
),D(2,π),弧
,
,
所在圆的圆心分别是(1,0),(1,
),(1,π),曲线M1是弧
,曲线M2是弧
,曲线M3是弧
。