一、选择题(本大题有10小题,每小题4分,共40分)
-
A . 5
B . -5
C .  D .
D . 
-
2.
(2019七上·余杭月考)
某市决定为全市中小学教室安装空调,今年预计投入资金126000000元,其中数字126000000用科学记数法可表示为( )
A . 12.6×107
B . 1.26×108
C . 1.26×109
D . 0.126×1010
-
-
4.
(2024九下·新会月考)
为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如下:
| 组别(cm) | x<160 | 160≤x<170 | 170≤x<180 | x≥180 |
| 人数 | 5 | 38 | 42 | 15 |
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180cm的概率是( )
A . 0.85
B . 0.57
C . 0.42
D . 0.15
-
5.
(2020七下·吉林月考)
如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( )
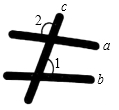
A . 5°
B . 10°
C . 30°
D . 70°
-
6.
若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于( )
A . -1
B . 0
C . 3
D . 4
-
7.
(2019·绍兴)
D在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线y=(x+3)(x-5),则这个变换可以是( )
A . 向左平移2个单位
B . 向右平移2个单位
C . 向左平移8个单位
D . 向右平移8个单位
-
8.
(2019·绍兴)
如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2

,则

的长为( )
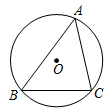
A . π
B .  π
C . 2π
D .
π
C . 2π
D .  π
π
-
9.
(2024八下·香洲期中)
正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
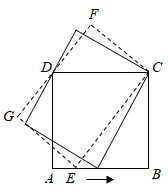
A . 先变大后变小
B . 先变小后变大
C . 一直变大
D . 保持不变
-
10.
(2019·绍兴)
如图1长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一楼进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
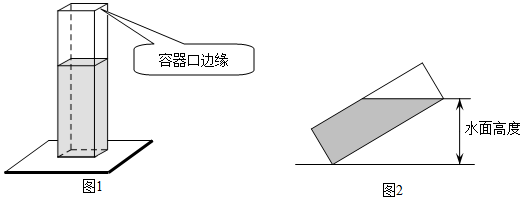
二、填空题(本大题有6小题,每小题5分,共30分)
-
-
-
13.
(2019·绍兴)
我国的《洛书》中记载着世界上最古老的一个幻方:将1~9这九个数字填入3×3的方格内,使三行、三列、角线的三个数之和都相等。如图幻方中,字母m所表示的数是
。
-
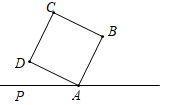
14.
(2019·绍兴)
如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧点A,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连结ED,则∠ADE的度数为
。
-
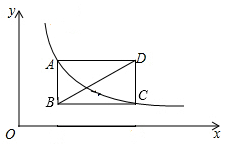
15.
(2019·绍兴)
如图,矩形ABCD的顶点A,C都在曲线y=

(常数k>0,x>0)上,若顶点D的坐标为(5,3),则直线BD的函数表达式是
.
-
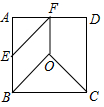
16.
(2019·绍兴)
把边长为2的正方形纸片ABCD分割成如图四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是
。
三、解答题(本大题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分。)
-
-
(1)
计算:4sin60°+(π-2)
0-(

)-

-
(2)
x为何值时,两个代数式x2+1,4x+1的值相等?
-
18.
(2019·绍兴)
如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象。
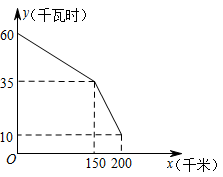
-
(1)
根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路。当0≤x≤150时,求1千瓦时的电量汽车能行驶的路程。
-
(2)
当150≤x≤200时,求y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量。
-
19.
(2020·三明模拟)
小明、小聪参加了100m跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图。
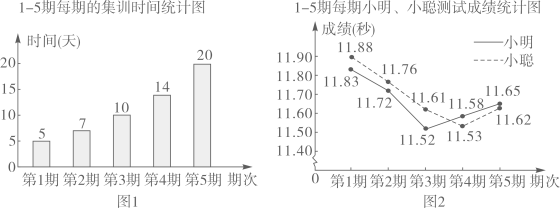
根据图中信息,解答下列问题:
-
(1)
这5期的集训共有多少天?小聪5次测试的平均成绩是多少?
-
(2)
根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.。
-
20.
(2019·绍兴)
如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上。
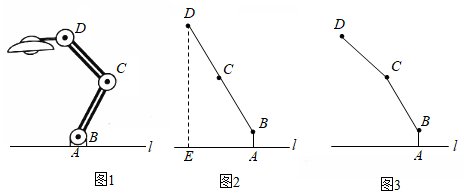
-
(1)
转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
-
(2)
将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:

≈1.41,

≈1.73)
-
21.
(2019·绍兴)
在屏幕上有如下内容:
如图,△ABC内接于⊙O,直径AB的长为2,过点C的切线交AB的题长线于点D.张老师要求添加条件后,编制一道题目,并解答。
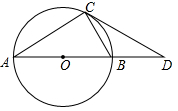
-
(1)
在屏幕内容中添加条件∠D=30°,求AD的长,请你解答。
-
(2)
以下是小明、小思的对话:
小明:我加的条件是BD=1,就可以求出AD的长。
小聪:你这样太简单了,我加的是∠A=30°,连结OC,就可证明△ACB与△DCO全等。
参考此对话:在屏幕内容中添加条件,编制一道题(可以添线、添字母),并解答。
-
22.
(2019·绍兴)
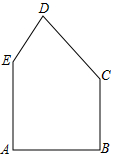
有一块形状如图的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°, ∠C=135°. ∠E>90°.要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大。
-
(1)
若所截矩形材料的一条边是BC或AE,求矩形材料的面积。
-
(2)
能否数出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.
-
23.
(2021九上·鹿城月考)
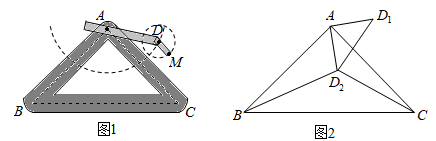
如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
-
(1)
在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
-
(2)
若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2.此时∠AD2C=135°,CD2=60,求BD2的长.
-
24.
(2019·绍兴)
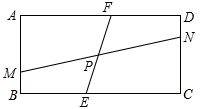
如图,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在边BC,AD上,MN,EF交于点P,记k=MN:EF.
-
(1)
若a:b的值为1,当MN⊥EF时,求k的值。
-
(2)
若a:b的值为

,求k的最大值和最小值。
-
(3)
若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a:b为的值。
 B .
B . 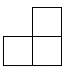 C .
C . 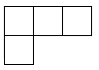 D .
D .