对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若 =N(a>0且a≠1),那么x叫做以a为底N的对数,记作x=logaN,比如指数式24=16可以转化为对数式4=log216,对数式2=log525,可以转化为指数式52=25.
我们根据对数的定义可得到对数的一个性质:
loga(M•N)=logaM+logaN(a>0,a≠1,M>0,N>0),理由如下:
设logaM=m,logaN=n,则M=am , N=an ,
∴M•N=am•an=am+n , 由对数的定义得m+n=loga(M•N)
又∵m+n=logaM+logaN
∴loga(M•N)=logaM+logaN
根据阅读材料,解决以下问题:
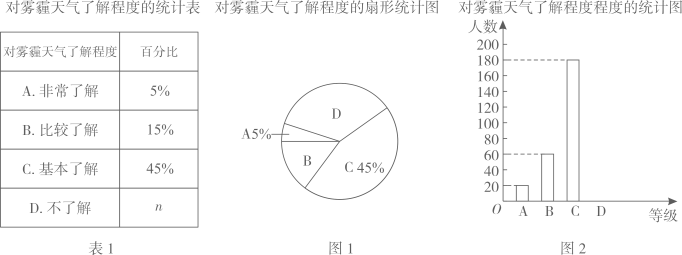
请结合统计图表,回答下列问题: