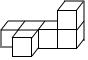
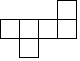
 C .
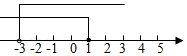
C . 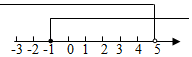 D .
D . 
| 施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
小明和小刚约定周末到某体育公园打羽毛球.他们两家到体育公园的距离分别是1200米,3000米,小刚骑自行车的速度是小明步行速度的3倍,若二人同时到达,则小明需提前4分钟出发,求小明和小刚两人的速度.
| | …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| | …… | 6 | 3 | 2 | 3 | 6 | …… |
乙写错了常数项,列表如下:
| | …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| | …… | ﹣2 | ﹣1 | 2 | 7 | 14 | …… |
通过上述信息,解决以下问题:
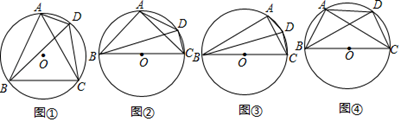
如图①,四边形 是
的内接四边形,连接
,
,
.求证:
.
小颖认为可用截长法证明:在 上截取
,连接
…
小军认为可用补短法证明:延长 至点
,使得
…
请你选择一种方法证明.
(探究1)
如图②,四边形 是
的内接四边形,连接
,
,
是
的直径,
.试用等式表示线段
,
,
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形 是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式.
如图④,四边形 是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式是.