山西省孝义市2018-2019学年七年级下学期数学期中考试试...

更新时间：2019-12-10 浏览次数：356 类型：期中考试

一、单选题

1. (2016七下·微山期中) 4的算术平方根是（）

A . 2 B . ﹣2 C . ±2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 如图，直线 $\text{[math]}$ ，直线 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 根据下列表述，能确定位置的是（）

A . 孝义市府前街 B . 南偏东 $\text{[math]}$ C . 美莱登国际影城3排 D . 东经 $\text{[math]}$ ，北纬 $\text{[math]}$

答案解析收藏纠错 + 选题
4. 下列说法正确的有（）
①对顶角相等；②同位角相等；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不相等，则这两个角一定不是同位角.

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. 如图，现要从村庄 $\text{[math]}$ 修建一条连接公路 $\text{[math]}$ 的最短小路，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，沿 $\text{[math]}$ 修建公路就能满足小路最短，这样做的依据是（）

A . 两点确定一条直线 B . 两点之间，线段最短 C . 垂线段最短 D . 平面内，过一点有且只有一条直线与已知直线垂直

答案解析收藏纠错 + 选题
6. 下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 在平面直角坐标系内，点 $\text{[math]}$ 的位置一定不在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
8. 如图，下列能判定 $\text{[math]}$ 的条件的个数是（）

① $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$ ④ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. 公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 $\text{[math]}$ ，导致了第一次数学危机. $\text{[math]}$ 是无理数的证明如下：
假设 $\text{[math]}$ 是有理数，那么它可以表示成 $\text{[math]}$ （ $\text{[math]}$ 与 $\text{[math]}$ 是互质的两个正整数）.于是 $\text{[math]}$ ，所以， $\text{[math]}$ .于是 $\text{[math]}$ 是偶数，进而 $\text{[math]}$ 是偶数.从而可设 $\text{[math]}$ ，所以 $\text{[math]}$ ， $\text{[math]}$ ，于是可得 $\text{[math]}$ 也是偶数.这与“ $\text{[math]}$ 与 $\text{[math]}$ 是互质的两个正整数”矛盾，从而可知“ $\text{[math]}$ 是有理数”的假设不成立，所以， $\text{[math]}$ 是无理数.这种证明“ $\text{[math]}$ 是无理数”的方法是（）

A . 综合法 B . 反证法 C . 举反例法 D . 数学归纳法

答案解析收藏纠错 + 选题
10. 规定以下两种变换：① $\text{[math]}$ ，如 $\text{[math]}$ ；② $\text{[math]}$ ，如 $\text{[math]}$ ，.按照以上变换有 $\text{[math]}$ .则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 比较大小： $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）.

答案解析收藏纠错 + 选题
12. 将命题“内错角相等”，写成“如果……，那么……”的形式：.

答案解析收藏纠错 + 选题
13. 平面直角坐标系的应用十分广泛，用坐标表示地理位置体现了坐标系在实际生活中的应用.不管是出差办事，还是出去旅游，人民都愿意带上一副地图，它给人们出行带来了很大方便.如图是某市地图的一部分.在图中，分别以正东、正北方向为 $\text{[math]}$ 轴， $\text{[math]}$ 轴的正方向建立平面直角坐标系，若表示牡丹园的点的坐标为 $\text{[math]}$ ，则表示狮虎园的点的坐标为.

答案解析收藏纠错 + 选题
14. 如果a，b是2019的两个平方根，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. 如图，半径为1个单位长度的圆从原点沿数轴向左滚动一周，圆上的一点由原点达到 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数是.

答案解析收藏纠错 + 选题
16. 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

17.
1. （1）计算： $\text{[math]}$
2. （2）计算： $\text{[math]}$
3. （3）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
18. 如图，四边形 $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 延长线上一点，点 $\text{[math]}$ 是边 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 和 $\text{[math]}$ 于点 $\text{[math]}$ 和点 $\text{[math]}$ .已知 $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ ，并写出每一步的根据.

答案解析收藏纠错 + 选题
19. 小丽想用一块面积为 $\text{[math]}$ 的正方形纸片，沿着边的方向裁出一块面积为 $\text{[math]}$ 的长方形纸片，使它的长宽之比为4:3，他不知道能否裁的出来，正在发愁，请你用所学知识帮小丽分析，能否裁出符合要求的纸片.

答案解析收藏纠错 + 选题
20. 如图，在平面直角坐标系中，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是三角形 $\text{[math]}$ 边 $\text{[math]}$ 上任意一点，三角形经过平移后得到三角形 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ .
1. （1）直接写出点 $\text{[math]}$ 的坐标.
2. （2）画出三角形 $\text{[math]}$ 平移后的三角形 $\text{[math]}$ .
3. （3）在 $\text{[math]}$ 轴上是否存在一点 $\text{[math]}$ ，使三角形 $\text{[math]}$ 的面积等于三角形 $\text{[math]}$ 面积的 $\text{[math]}$ ，若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题

21. 阅读与探究:

在第六章《实数》中，我们学习了平方根和立方根.下表是平方根和立方根的部分内容.

	平方根	立方根
定义	一般地，如果一个数的平方等于 $\text{[math]}$ ，那么这个数叫做 $\text{[math]}$ 的平方根或二次方根.这就是说，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 叫做 $\text{[math]}$ 的平方根.	一般地，如果一个数的立方等于 $\text{[math]}$ ，那么这个数叫做 $\text{[math]}$ 的立方根或三次方根.这就是说，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 叫做 $\text{[math]}$ 的立方根.
运算	求一个数 $\text{[math]}$ 的平方根的运算，叫做开平方.开平方与平方互为逆运算.	求一个数 $\text{[math]}$ 的平立方根的运算，叫做开立方.开立方与立方互为逆运算.
特征	正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.	正数的立方根是正数；0的立方根是0；负数的立方根是负数.
表示与读法	正数 $\text{[math]}$ 的平方根可以用“ $\text{[math]}$ ”表示，读作“正负根号 $\text{[math]}$ ”.	一个数 $\text{[math]}$ 的立方根可以用“ $\text{[math]}$ ”表示，读作“三次根号 $\text{[math]}$ ”.

今天我们类比平方根和立方根的学习方法学习四次方根.

（1） ①填表
$\text{[math]}$
1
16
$\text{[math]}$
$\text{[math]}$
②结合上述①中表格情况，类比平方根和立方根的定义，给四次方根下定义：
（2）思考与归纳
求一个数 $\text{[math]}$ 的四次方根的运算叫做开四次方.开四次方和四次方运算互为逆运算.

①探究：

81的四次方根是； $\text{[math]}$ 的四次方根是；

0的四次方根是； $\text{[math]}$ （填“有”或“没有”）四次方根.

②归纳：

根据上述①中情况，类比平方根和立方根的特征，归纳四次方根的特征：

③总结：

我们归纳四次方根的特征时，分了正数、0、负数三类进行研究，这种思想叫；（填正确选项的代码）

四次方根的特征是由81， $\text{[math]}$ ，0等这几个特殊数的四次方根的特征归纳出来的，这种思想叫.（填正确选项的代码）

A.类比思想

B.分类讨论思想

C.由一般到特殊的思想

D.由特殊到一般的思想
（3）巩固与应用
类似于平方根和立方根，一个数 $\text{[math]}$ 的四次方根，用符号“ $\text{[math]}$ ”表示，读作“正、负四次根号 $\text{[math]}$ ”，其中 $\text{[math]}$ 是被开方数，4是根指数.例如 $\text{[math]}$ 表示16的四次方根， $\text{[math]}$ .

① $\text{[math]}$ （将结果直接填到横线上）.

②比较大小： $\text{[math]}$ $\text{[math]}$ （填“”或“”或“”）.

答案解析收藏纠错 + 选题

22. 综合与实践：折纸中的数学
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题，并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定，今天我们继续探究：折纸中的数学——长方形纸条的折叠与平行线.
1. （1）
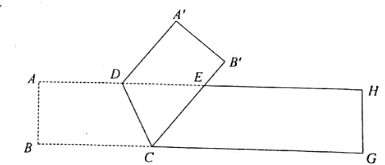
  知识初探
  如图1，长方形纸条 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .将长方形纸条沿直线 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，点 $\text{[math]}$ 落在 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
2. （2）
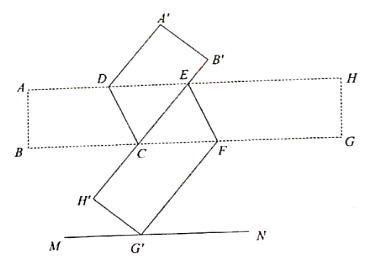
  类比再探
  如图2，在图1的基础上将 $\text{[math]}$ 对折，点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上的 $\text{[math]}$ 处.点 $\text{[math]}$ 落在 $\text{[math]}$ 处，得到折痕 $\text{[math]}$ ，则折痕 $\text{[math]}$ 与 $\text{[math]}$ 有怎样的位置关系？说明理由.
3. （3）
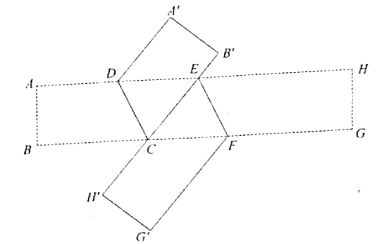
  拓展延伸
  如图3，在图2的基础上，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线 $\text{[math]}$ ，请你猜想 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由.
答案解析收藏纠错 + 选题