内蒙古鄂尔多斯康巴什新区2018-2019学年九年级上学期数...

更新时间：2019-10-14 浏览次数：250 类型：期中考试

一、单选题

1. (2018九上·康巴什期中) 如图：下列四个图案中既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020九上·东莞期中) 已知m是方程x²﹣x﹣1=0的一个根，则代数式m²﹣m的值等于（）

A . ﹣1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
3. (2021九上·费县月考) 三角形两边长分别是8和6，第三边长是一元二次方程x²﹣16x+60=0一个实数根，则该三角形的面积是（）

A . 24 B . 48 C . 24或8 $\text{[math]}$ D . 8 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·西和期中) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·昌平期末) 下列语句中错误的有（）
①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③圆是轴对称图形，任何一条直径都是它的对称轴；④长度相等的两条弧是等弧

A . 3个 B . 2个 C . 1个 D . 4个

答案解析收藏纠错 + 选题
6. (2020九上·翼城期末) 如图，在Rt△ABO中，AB⊥OB，且AB=OB=3，设直线x=t截此三角形所得的阴影部分的面积为S，则S与t之间的函数关系式为（）

A . S=t(0＜t≤3) B . S= $\text{[math]}$ t²(0＜t≤3) C . S=t²(0＜t≤3) D . S= $\text{[math]}$ t²-1(0＜t≤3)

答案解析收藏纠错 + 选题
7. (2021九上·嘉祥月考) 在同一坐标系内，一次函数y=ax+b与二次函数y=ax²+8x+b的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2018九上·康巴什期中) 如图，△ABC中，∠ACB=90°∠A=25°，若以点C为旋转中心，将△ABC旋转到△DEC的位置，点B在边DE上，则旋转角的度数是（）

A . 50° B . 55° C . 65° D . 70°

答案解析收藏纠错 + 选题
9. (2020九上·长沙月考) 如图，AB为⊙O直径，已知为∠DCB=20°，则∠DBA为（）

A . 50° B . 20° C . 60° D . 70°

答案解析收藏纠错 + 选题
10. (2019九上·绵阳期中) 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（）

A . 3cm B . $\text{[math]}$ cm C . 2.5cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·康巴什期中) 已知二次函数 $\text{[math]}$ 的图象和 $\text{[math]}$ 轴有交点，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
12. (2018九上·康巴什期中) 若点 $\text{[math]}$ 与 $\text{[math]}$ 关于原点对称，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2021·牡丹江) 半径等于12的圆中，垂直平分半径的弦长为．

答案解析收藏纠错 + 选题
14. (2018九上·康巴什期中) 如图，若抛物线y=ax²+bx+c上的P（4，0），Q两点关于它的对称轴x=1对称，则关于x的一元二次方程ax²+bx+c=0的解是．

答案解析收藏纠错 + 选题
15. (2023·永善模拟) 如下图，正方形ABCD的边AB在x轴上，A（﹣4，0），B（﹣2，0），定义：若某个抛物线上存在一点P，使得点P到正方形ABCD四个顶点的距离相等，则称这个抛物线为正方形ABCD的“友好抛物线”．若抛物线y=2x²﹣nx﹣n²﹣1是正方形ABCD的“友好抛物线”，则n的值为．

答案解析收藏纠错 + 选题
16. (2018九上·康巴什期中) 如图，在平面直角坐标系中，可通过平移抛物线y= $\text{[math]}$ x²得到抛物线y= $\text{[math]}$ x²﹣2x，其对称轴与两段抛物线所围成的阴影部分（如图所示）的面积是.

答案解析收藏纠错 + 选题

三、解答题

17. (2018九上·康巴什期中) 解方程：
1. （1） x²-4x-5=0
2. （2） 3x²-6x+4=0
答案解析收藏纠错 + 选题
18. (2018九上·康巴什期中) 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：
1. （1）试作出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB₁C₁；点B₁的坐标为；
2. （2）作△ABC关于原点O成中心对称的△A₂B₂C₂；点B₂的坐标为.
答案解析收藏纠错 + 选题
19. (2021八下·北票期中) 如图，将△ABC绕点B逆时针旋转α得到△DBE，DE的延长线与AC相交于点F，连接DA、BF，∠ABC=α=60°，BF=AF．
1. （1）求证：DA∥BC；
2. （2）猜想线段DF、AF的数量关系，并证明你的猜想．
答案解析收藏纠错 + 选题
20. (2018九上·康巴什期中) 图中是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，建立如图所示的平面直角坐标系：
1. （1）求拱桥所在抛物线的解析式；
2. （2）当水面下降1m时，则水面的宽度为多少？
答案解析收藏纠错 + 选题
21. (2018九上·康巴什期中) 在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F，且CF⊥AD.
求∠D的度数.

答案解析收藏纠错 + 选题
22. (2018九上·康巴什期中) 某商场销售一种商品，进价为每个20元，规定每个商品售价不低于进价，且不高于60元.经调查发现，每天的销售量y(个）与每个商品的售价x(元）满足一次函数关系，其部分数据如下表所示：
1. （1）求y与x之间的函数关系式；
2. （2）设商场每天获得的总利润为w（元），求w与x之间的函数关系式；
3. （3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
答案解析收藏纠错 + 选题
23. (2018九上·康巴什期中) 如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C，D两点.点P是x轴上的一个动点.
1. （1）求此抛物线的解析式；
2. （2）当PA+PB的值最小时，求点P的坐标；
3. （3）抛物线上是否存在一点Q(Q与B不重合)，使△CDQ的面积等于△BCD的面积？若存在，直接写出点Q的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
24. (2018九上·康巴什期中) （问题解决）
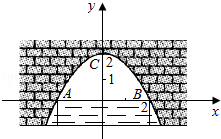
一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．你能求出∠APB的度数吗？
小明通过观察、分析、思考，形成了如下思路：
1. （1）思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；
  思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．
  请参考小明的思路，任选一种写出完整的解答过程．
2. （2）【类比探究】
  如图2，若点P是正方形ABCD外一点，PA=3，PB=1，PC= $\text{[math]}$ ，求∠APB的度数．
答案解析收藏纠错 + 选题