浙江省温州市瑞安市2019届数学中考一模试卷

更新时间：2024-07-13 浏览次数：596 类型：中考模拟

一、单选题

1. 下列选项中的实数，属于无理数的是（）

A . $\text{[math]}$ B . 0.36 C . $\text{[math]}$ D . ﹣2

答案解析收藏纠错 + 选题
2. 如图，桌面上放着一个一次性纸杯，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021七下·保定期中) 计算：m⁶•m²的结果为（）

A . m¹² B . m⁸ C . m⁴ D . m³

答案解析收藏纠错 + 选题
4. 在平面直角坐标系中，点A（﹣1，2）位于（）

A . 第四象限 B . 第三象限 C . 第二象限 D . 第一象限

答案解析收藏纠错 + 选题
5. 某市4月份第一周每天最高气温（℃）分别为：19，19，22，24，19，20，24，则该市这一周每天最高气温的众数和中位数分别是（）

A . 19，22 B . 24，20 C . 19，24 D . 19，20

答案解析收藏纠错 + 选题
6. 不等式x﹣1＜2的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. 若关于x的方程x²+x﹣a+ $\text{[math]}$ =0有两个不相等的实数根，则实数a的取值范围是（）

A . a＞2 B . a≥2 C . a≤2 D . a＜2

答案解析收藏纠错 + 选题
8. 如图，已知△ABC的三个顶点均在正方形网格的格点上，则tanA的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·瑞安模拟) 如图，在正方形ABCD中，E，F分别是AB，CD的中点，EG⊥AF，FH⊥CE，垂足分别为G，H，设AG＝x，图中阴影部分面积为y，则y与x之间的函数关系式是（）

A . y＝3 $\text{[math]}$ x² B . y＝4 $\text{[math]}$ x² C . y＝8x² D . y＝9x²

答案解析收藏纠错 + 选题
10. 如图，C是以AB为直径的半圆上的一动点，分别以AC，BC为边在△ABC的内侧和外侧作正方形ACDE，正方形BCFH.在点C沿半圆从点A运动到半圆中点M的过程中（点C不与点A，M重合）.四边形AEBH的面积变化情况是（）

A . 先减小后增大 B . 不变 C . 先增大后减小 D . 一直增大

答案解析收藏纠错 + 选题

二、填空题

11. (2022七下·宁波期中) 因式分解：x²﹣9=．

答案解析收藏纠错 + 选题
12. 圆心角为120°，半径为2的扇形，则这个扇形的面积为.

答案解析收藏纠错 + 选题
13. 一个不透明的布袋里装有若干个只有颜色不同的红球和白球，其中3个红球，且从布袋中随机摸出1个球，摸出的球是红球的概率是 $\text{[math]}$ ，则白球的个数是

答案解析收藏纠错 + 选题
14. 某校组织1080名学生去外地参观，现有A、B两种不同型号的客车可供选择.每辆B型客车的载客量比每辆A型客车多坐15人，若只选择B型客车比只选择A型客车少租12辆（每辆客车均坐满）.设B型客车每辆坐x人，则列方程为.

答案解析收藏纠错 + 选题
15. 七巧板是一种古老的中国传统智力游戏.小明利用七巧板（如图1）拼出了一个数字“7”（如图2），若图1中正方形ABCD的面积为32cm² ，则图2的周长为cm

答案解析收藏纠错 + 选题
16. 如图所示，在平面直角坐标系xOy中，Rt△ABC的直角顶点C在第一象限，CB⊥x轴于点B，点A在第二象限，AB与y轴交于点G，且满足AG＝OG＝ $\text{[math]}$ BG，反比例函数y＝ $\text{[math]}$ 的图象分别交BC，AC于点E，F，CF＝ $\text{[math]}$ k.以EF为边作等边△DEF，若点D恰好落在AB上时，则k的值为

答案解析收藏纠错 + 选题

三、解答题

17. (2020·惠山模拟)
1. （1）计算：（ $\text{[math]}$ ﹣1）⁰+3×（﹣2）+ $\text{[math]}$
2. （2）化简：（x+2）²﹣x（x+2）
答案解析收藏纠错 + 选题
18. (2019·瑞安模拟) 如图，在▱ABCD中，E，F分别为边AB，CD的中点，BD是对角线.
1. （1）求证：△ADE≌△CBF；
2. （2）若∠ADB＝90°，AB＝6，求四边形BEDF的周长.
答案解析收藏纠错 + 选题
19. (2019·瑞安模拟) 共享单车是一种新型环保的交通工具，为市民的出行带来了极大的方便.某市中学生对市民共享单车的使用情况进行了问卷调查，并将这次调查情况整理、绘制成如图两幅统计图（部分信息未给出）.根据图中的信息，解答下列问题：
1. （1）这次活动中接受问卷调查的市民共有名；
2. （2）补全条形统计图，并计算扇形统计图中的D类的扇形圆心角为度；
3. （3）根据统计结果，若该市市区有80万市民，请估算利用单车“外出游玩“的人数.
答案解析收藏纠错 + 选题
20. (2019·瑞安模拟) 6×6网格按如图所示放置在平面直角坐标系中（网格的两条邻边界与坐标轴重合），已知点A（1，4），B（5，1），请在所给的网格内（含边界）按要求画格点△PAB（三角形的顶点都在小正方形的顶点上），并写出点P的坐标.
1. （1）在图1中画一个格点等腰△PAB，此时点P的坐标是；
2. （2）在图2中画一个格点直角△PAB，使点P在第一象限内，此时点P的坐标是；
3. （3）在图3中画一个面积为5的格点直角△PAB，此时点P的坐标是.
答案解析收藏纠错 + 选题
21. (2019·瑞安模拟) 如图，在平面直角坐标系中，抛物线y＝﹣x²+bx+c经过原点O，对称轴为直线x＝2，与x轴的另一个交点为A，顶点为B.
1. （1）求该抛物线解析式并写出顶点B的坐标；
2. （2）过点B作BC⊥y轴于点C，若抛物线上存在点P，Q使四边形BCPQ为平行四边形，请判断点P是否在直线AC上？说明你的理由.
答案解析收藏纠错 + 选题
22. (2019·瑞安模拟) 如图，AB为⊙O的直径，点C是⊙O上一点，CD是⊙O的切线，∠CDB＝90°，BD交⊙O于点E.
1. （1）求证： $\text{[math]}$ .
2. （2）若AE＝12，BC＝10.
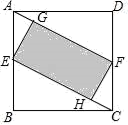
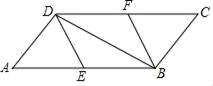
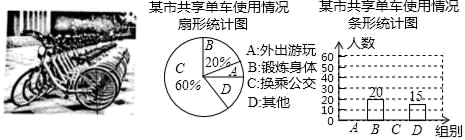
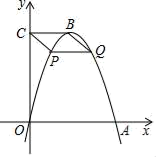
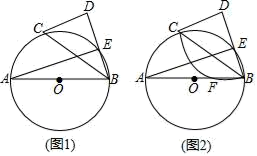
  ①求AB的长；
  
  ②如图2，将 $\text{[math]}$ 沿弦BC折叠，交AB于点F，则AF的长为。
答案解析收藏纠错 + 选题
23. (2019·瑞安模拟) 如图是一款自动热水壶，其工作方式是：常规模式下，热水壶自动加热到100℃时自动停止加热，随后转入冷却阶段，当水温降至60℃时，热水壶又自动开始加热，…，重复上述程序，若在冷却过程中按下“再沸腾”键，则马上开始加热，加热到100℃后又重复上述程序，现对加热到100℃开始，冷却到60℃再加热100℃这一过程中水温y（℃）与所需时间x（分）进行测量记录，发现在冷却过程中满足y＝ $\text{[math]}$ x²﹣2x+100，加热过程中水温y（℃）与时间x（分）也满足一定的函数关系，记录的部分数据如表：

时间x（分）

…

41

42

45

47

…

水温y（℃）

…

65

70

85

95

…

根据题中提供的信息，解答下列问题：
1. （1）求水温从100℃冷却到60℃所需的时间；
2. （2）请你从学过的函数中确定，哪种函数能表示加热过程中水温y（℃）与时间x（分）之间的变化规律，并写出函数表达式.
3. （3）在一次用水过程中，小明因急需100℃的热水而在冷却过程中使用了“再沸腾”键，结果使水温到达100℃的时间比常规模式缩短了22分钟，求小明按下“再沸腾”键时的水温.
答案解析收藏纠错 + 选题
24. (2019·瑞安模拟) 如图，在平面直角坐标系中，点O为坐标原点，点A的坐标为（﹣3，0），点B的坐标为（2，0）.在y轴正半轴上有一动点C，△ABC的外接圆与y轴的另一交点为D.过点A作直线BC的垂线，垂足为E，直线AE交y轴于点F.
1. （1）求证：OF＝OD
2. （2）随着点C的运动，当∠ACB是钝角时，是否存在CO＝CE的情形？若存在，试求OD的长；若不存在，请说明理由.
3. （3）将点B绕点F顺时针旋转90°得到点G，在点C的整个运动过程中.
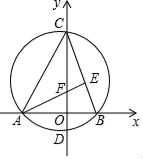
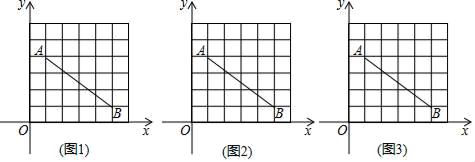
  ①当点G恰好落在△ABC的边AC或边BC所在直线上时，求满足条件的点C坐标.
  
  ②当CG∥AB时，则△ABC的面积是（直接写出结果）
答案解析收藏纠错 + 选题