云南省易门县2019届九年级上学期数学期中考试试卷

更新时间：2024-07-13 浏览次数：345 类型：期中考试

一、单选题

1. (2023九上·张湾期中) 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2018九上·易门期中) 下列方程中，属于一元二次方程的是（）

A . ax²+bx+c=0 B . $\text{[math]}$ C . （x+3）²=2（x﹣3） D . （x+4）（x﹣2）=x²

答案解析收藏纠错 + 选题
3. (2018九上·易门期中) 已知函数 $\text{[math]}$ 是二次函数，则 $\text{[math]}$ 等于（）

A . ±2 B . 2 C . -2 D . ±1

答案解析收藏纠错 + 选题
4. (2018九上·易门期中) 如图，将 $\text{[math]}$ 绕直角顶点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·杭州期末) 一元二次方程x²﹣6x﹣5=0配方可变形为（）

A . （x﹣3）²=14 B . （x﹣3）²=4 C . （x+3）²=14 D . （x+3）²=4

答案解析收藏纠错 + 选题
6. (2019九上·禹城期中) 当ab＞0时，y＝ax²与y＝ax＋b的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2018九上·易门期中) 二次函数 $\text{[math]}$ 的图象如图所示，则下
列结论：① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ ，⑤ $\text{[math]}$ $\text{[math]}$ 中正确的是（）

A . ②④⑤ B . ①②④ C . ①③④ D . ①③④⑤

答案解析收藏纠错 + 选题

二、填空题

8. (2018九上·易门期中) 已知点M的坐标为（－2，－3），则点M关于原点对称的坐标为．

答案解析收藏纠错 + 选题
9. (2019九上·昭通期中) 一元二次方程（x+1）(3x－2)=8的一般形式是 .

答案解析收藏纠错 + 选题
10. (2018九上·易门期中) 已知抛物线的顶点为（1，﹣3），且过点（2，1），求这个函数的表达式为.

答案解析收藏纠错 + 选题
11. (2018九上·易门期中) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两实数根之积为负，则实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
12. (2018九上·易门期中) 设 A（﹣2，y₁），B（1，y₂），C（2，y₃）是抛物线 y=（x﹣1）²﹣3上的三点，则 y₁ ， y₂ ， y₃ 的大小关系为.

答案解析收藏纠错 + 选题
13. (2021九上·抚远期中)
如图，两块相同的三角板完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D=

答案解析收藏纠错 + 选题

三、解答题

14. (2019九上·如东月考) 解方程：
1. （1） 2x²﹣5x﹣3=0
2. （2）（x﹣3）²+2x（x﹣3）=0.
答案解析收藏纠错 + 选题
15. (2020九上·江川期末) 组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，则比赛组织者应邀请多少个队参赛？

答案解析收藏纠错 + 选题
16. (2020九上·鼓楼月考) 如图，在△ABC中，∠C＝90°，AC＝2cm，AB＝3cm，将△ABC绕点B顺时针旋转60°得到△FBE，求点E与点C之间的距离.

答案解析收藏纠错 + 选题
17. (2018九上·易门期中) 把二次函数y=a(x-h)²+k的图象先向左平移2个单位，再向上平移4个单位，得到二次函数y= $\text{[math]}$ (x+1)²-1的图象.
1. （1）试确定a，h，k的值；
2. （2）指出二次函数y=a(x-h)²+k的开口方向，对称轴和顶点坐标.
答案解析收藏纠错 + 选题
18. (2021九上·广汉期中) 已知关于x的方程x²－(k＋2)x＋2k＝0．
1. （1）求证：k取任何实数值，方程总有实数根；
2. （2）若Rt△ABC斜边长a＝3，另两边长b，c恰好是这个方程的两个根，求△ABC的周长．
答案解析收藏纠错 + 选题
19. (2019九上·罗平期中) 在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元.
1. （1）求每张门票原定的票价；
2. （2）根据实际情况，活动组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率.
答案解析收藏纠错 + 选题
20. (2018九上·易门期中) 某商场销售一批名牌衬衫，平均每天可售出 20 件，每件盈利 45 元，为了扩大销售、增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价 1 元.商场平均每天可多售出 4 件，
1. （1）若商场平均每天盈利最大，每件衬衫应降价多少元？
2. （2）每天可售出多少件？
答案解析收藏纠错 + 选题
21. (2018九上·易门期中) 如图，在边长为1的小正方形网格中，△AOB的顶点均在格点上，
1. （1） B点关于y轴的对称点坐标为；
2. （2） ①将△AOB向左平移3个单位长度得到△A₁O₁B₁ ，请画出△A₁O₁B₁；
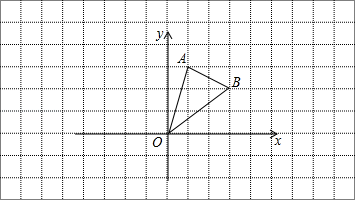
  ②以原点O为对称中心，画出△ AOB与关于原点成中心对称的△ A₂ O B₂；
  
  ③以原点O为旋转中心，画出把△AOB顺时针旋转90°的图形△A₃ O B₃.
答案解析收藏纠错 + 选题
22. (2018九上·易门期中) 如图，抛物线y＝ax²+3x+c经过A（﹣1，0），B（4，0）两点，与y轴交于点C.
1. （1）求抛物线的解析式；
2. （2）若点P在第一象限的抛物线上，且点P的横坐标为t，过点P向x轴作垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式，并求出m的最大值；
3. （3）在x轴上是否存在点E，使以点B，C，E为顶点的三角形为等腰三角形？如果存在，直接写出E点坐标；如果不存在，请说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

云南省易门县2019届九年级上学期数学期中考试试卷

副标题：

*注意事项：

云南省易门县2019届九年级上学期数学期中考试试卷

试题分析

总体分析

题量分析

难度分析

知识点分析