浙江省杭州市余杭区2019-2020学年八年级上学期数学第一...

更新时间：2024-07-13 浏览次数：315 类型：月考试卷

一、选择题（每小题3分，共30分）

1. (2020七下·吉林月考) 如图，墙上钉着三根木条，a，b，c，量得∠1=70°，∠2=100°，那么木条a，b所在直线所夹的锐角是（）

A . 5° B . 10° C . 30° D . 70°

答案解析收藏纠错 + 选题
2. (2024八上·雷州月考) 下列长度的3根小木棒不能搭成三角形的是（）

A . 2cm，3cm，4cm B . 1cm，2cm，3cm C . 3cm，4cm，5cm D . 4cm，5cm，6cm

答案解析收藏纠错 + 选题
3. (2019八上·余杭月考) 能说明命题“若|a|=|b|，则a=b”是假命题的反例为（）

A . a=2,b=-2 B . a=1,b=0 C . a=1,b=1 D . a=-3,b= $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019八上·浙江期中) 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线。则对应作法错误的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
5. (2020八上·乌拉特前旗期中) 如图，△ABC≌△DEF，若 BC=12cm，BF=16cm，则下列判断错误的是（）

A . AB=DE B . BE=CF C . AB//DE D . EC=4cm

答案解析收藏纠错 + 选题
6. (2019八上·余杭月考) 如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（）

A . 40° B . 45° C . 50° D . 60°

答案解析收藏纠错 + 选题
7. (2020八上·湛江期中) 下列图形中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2023八上·鄞州期末) “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）

A . 60° B . 65° C . 75° D . 80°

答案解析收藏纠错 + 选题
9. (2019八上·余杭月考) 将一根长24cm的筷子置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为h，则h的取值范围是（）

A . 12cm≤h≤19cm B . 12cm≤h≤13cm C . 11cm≤h≤12cm D . 5cm≤h≤12cm

答案解析收藏纠错 + 选题
10. (2019八上·余杭月考) 如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，连结CE交AD于点F，连结BD交CE于点G，连结BE．下列结论中，正确的结论有（）

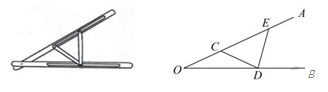
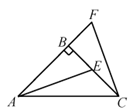
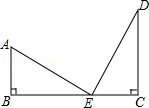
①CE=BD； ②△ADC是等腰直角三角形；③∠ADB=∠AEB；④S_{四边形BCDE}= $\text{[math]}$ BD•CE；⑤BC²+DE²=BE²+CD² ．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共24分）

11. (2019八上·余杭月考) 如图，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1+∠2＝度.

答案解析收藏纠错 + 选题
12. (2024八上·唐山月考) 在△ABC中，∠A=50°，∠B=30°，点D在AB边上，连接CD，若△ACD为直角三角形，则∠BCD的度数为度．

答案解析收藏纠错 + 选题
13. (2024八下·锦州期中) 定义：等腰三角形的顶角与其一个底角的度数的比值 $\text{[math]}$ 称为这个等腰三角形的“特征值”.若等腰 $\text{[math]}$ 中， $\text{[math]}$ ，则它的特征值 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2020九下·长沙开学考) 如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=度.

答案解析收藏纠错 + 选题
15. (2019八上·余杭月考) 已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA ，垂足为点E ，且直线DE交OB于点F ，如图所示．若DE＝2，则DF＝．

答案解析收藏纠错 + 选题
16. (2020九上·临泽期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ．若将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 与边 $\text{[math]}$ 的中点 $\text{[math]}$ 恰好重合，则四边形 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题

三、解答题（本大题有7小题，共66分）

17. (2021八上·淮滨月考) 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）

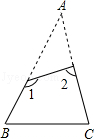
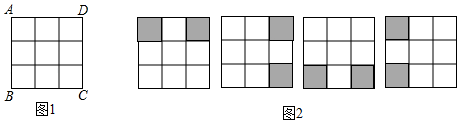
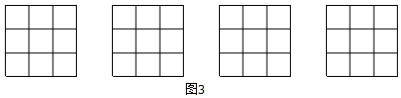
请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）

答案解析收藏纠错 + 选题
18. (2023八上·市中区月考) 如图，有两根长杆隔河相对，一杆高3m，另一杆高2m，两杆相距5m．两根长杆都与地面垂直，现两杆顶部各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮出一条小鱼，于是同时以同样的速度飞下来夺鱼，结果两只鱼鹰同时叼住小鱼．求两杆底部距小鱼的距离各是多少米．（假设小鱼在此过程中保持不动）

答案解析收藏纠错 + 选题
19. (2022八上·南昌期中) 如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F.
1. （1）若∠C＝36°，求∠BAD的度数；
2. （2）求证：FB＝FE.
答案解析收藏纠错 + 选题
20. (2019八上·余杭月考) 在如图所示的网格中有四条线段AB、CD、EF、GH（线段端点在格点上），
1. （1）选取其中三条线段，使得这三条线段能围成一个直角三角形．
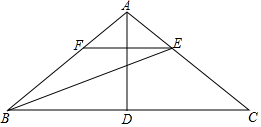
  答：选取的三条线段为．
2. （2）只变动其中两条线段的位置，在原图中画出一个满足上题的直角三角形（顶点仍在格点，并标上必要的字母）．
  答：画出的直角三角形为△．
3. （3）所画直角三角形的面积为．
答案解析收藏纠错 + 选题
21. (2019八上·余杭月考) 如图
1. （1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则∠AEB的度数为，线段AD、BE之间的关系．
2. （2）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．①请判断∠AEB的度数，并说明理由；②当CM=5时，AC比BE的长度多6时，求AE的长．
答案解析收藏纠错 + 选题
22. (2019八上·余杭月考) 如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•
1. （1）求证：△ABD≌△ECB；
2. （2）若∠EDC=65°，求∠ECB的度数；
3. （3）若AD=3，AB=4，求DC的长.
答案解析收藏纠错 + 选题
23. (2019八上·余杭月考) 联想三角形外心的概念，我们可引入如下概念。
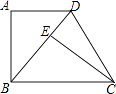
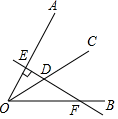
定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。

举例：如图1，若PA=PB，则点P为△ABC的准外心。

应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD= $\text{[math]}$ AB，求∠APB的度数。

探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长。

答案解析收藏纠错 + 选题