![]()
 B .
B .  C .
C . ![]()
动时间(小时) | 3 | 3.5 | 4 | 4.5 |
人数 | 1 | 1 | 2 | 1 |
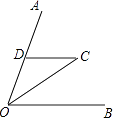
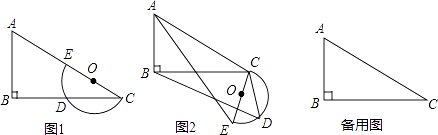
①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )

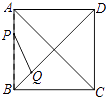
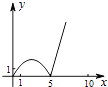
如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )
 B .
B . 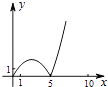 C .
C . 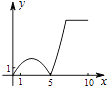 D .
D . 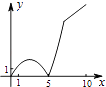

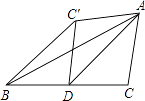
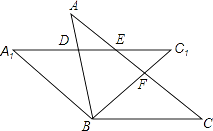
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD=,对角线MN长度的最小值为.

月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
从上表可知,每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
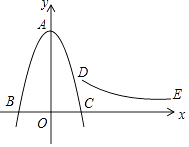
如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1 , 且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2 .