2017年贵州省安顺市中考数学六模试卷

更新时间：2024-07-12 浏览次数：637 类型：中考模拟

一、选择题

1. (2019·南山模拟) $\text{[math]}$ 的相反数是（）

A . 2 B . ﹣2 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·安顺模拟) 下列计算正确的是（）

A . x+x²=x³ B . x²•x³=x⁶ C . （x³）²=x⁶ D . x⁶÷x³=x²

答案解析收藏纠错 + 选题
3. (2017·安顺模拟) 为了解某社区居民的用电情况，随机对该社区10户居民进行调查，下表是这10户居民2015年4月份用电量的调查结果：
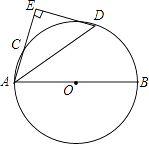
居民（户）
1
2
3
4
月用电量（度/户）
30
42
50
51
那么关于这10户居民月用电量（单位：度），下列说法错误的是（）

A . 中位数是50 B . 众数是51 C . 方差是42 D . 极差是21

答案解析收藏纠错 + 选题
4. (2017·安顺模拟)
如图，AB∥CD，EF与AB、CD分别相交于点E、F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP=50°，则∠EPF=（　　）度．

A . 70 B . 65 C . 60 D . 55

答案解析收藏纠错 + 选题
5. (2017·安顺模拟) 今年五月份香港举办“保普选反暴力”大联盟大型签名活动，9天共收集121万个签名，将121万用科学记数法表示为（）

A . 1.21×10⁶ B . 12.1×10⁵ C . 0.121×10⁷ D . 1.21×10⁵

答案解析收藏纠错 + 选题
6. (2017·安顺模拟) 在Rt△ABC的直角边AC边上有一动点P（点P与点A，C不重合），过点P作直线截得的三角形与△ABC相似，满足条件的直线最多有（）

A . 1条 B . 2条 C . 3条 D . 4条

答案解析收藏纠错 + 选题
7. (2017·乌鲁木齐模拟) 如图为二次函数y=ax²+bx+c（a≠0）的图象，则下列说法：
①a＞0 ②2a+b=0 ③a+b+c＞0 ④当﹣1＜x＜3时，y＞0
其中正确的个数为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2020九上·宁阳期中) 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）

A . 3：4 B . 9：16 C . 9：1 D . 3：1

答案解析收藏纠错 + 选题
9. (2018·福田模拟) 如图，将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′，点B经过的路径为弧BB′，若∠BAC=60°，AC=1，则图中阴影部分的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . π

答案解析收藏纠错 + 选题

二、填空题

10. (2017·安顺模拟) 在实数范围内分解因式：x³﹣2x=

答案解析收藏纠错 + 选题
11. (2017·安顺模拟) 已知x+ $\text{[math]}$ =2，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2019·新田模拟) 从﹣1、0、 $\text{[math]}$ 、0.3、π、 $\text{[math]}$ 这六个数中任意抽取一个，抽取到无理数的概率为．

答案解析收藏纠错 + 选题
13. 已知点P（3，a）关于y轴的对称点为Q（b，2），则ab=．

答案解析收藏纠错 + 选题
14. (2019·越秀模拟) 关于x的一元二次方程x²﹣x+m=O没有实数根，则m的取值范围是．

答案解析收藏纠错 + 选题
15. (2017·安顺模拟) 如图，在菱形ABCD中，点P是对角线AC上的一点，PE⊥AB于点E．若PE=3，则点P到AD的距离为．

答案解析收藏纠错 + 选题
16. (2017·安顺模拟)
如图是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成，第（1）个图案有4个三角形，第（2）个图案有7个三角形，第（3）个图案有10个三角形，…依此规律，第n个图案有个三角形（用含n的代数式表示）

答案解析收藏纠错 + 选题

三、解答题

17. (2017·安顺模拟) 计算：（﹣2016）⁰+（ $\text{[math]}$ ）^﹣¹+| $\text{[math]}$ ﹣2|﹣2cos60°．

答案解析收藏纠错 + 选题
18. (2017·安顺模拟) 先化简，再求值：（ $\text{[math]}$ +2﹣x）÷ $\text{[math]}$ ，其中x满足x²﹣4x+3=0．

答案解析收藏纠错 + 选题
19. (2017·安顺模拟) 某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．
1. （1）根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．
2. （2）问血液中药物浓度不低于4微克/毫升的持续时间多少小时？
答案解析收藏纠错 + 选题
20. (2017·安顺模拟) ”切实减轻学生课业负担”是我市作业改革的一项重要举措．某中学为了解本校学生平均每天的课外作业时间，随机抽取部分学生进行问卷调查，并将调查结果分为A、B、C、D四个等级，A：1小时以内；B：1小时﹣﹣1.5小时；C：1.5小时﹣﹣2小时；D：2小时以上．根据调查结果绘制了如图所示的两种不完整的统计图，
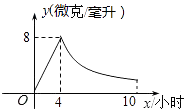
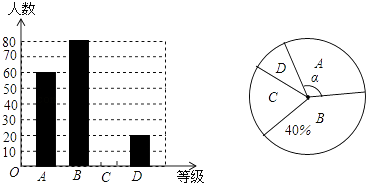
请根据图中信息解答下列问题：
1. （1）该校共调查了学生；
2. （2）请将条形统计图补充完整；
3. （3）表示等级A的扇形圆心角α的度数是；
4. （4）在此次调查问卷中，甲、乙两班各有2人平均每天课外作业量都是2小时以上，从这4人中人选2人去参加座谈，用列表表或画树状图的方法求选出的2人来自不同班级的概率．
答案解析收藏纠错 + 选题
21. (2017·安顺模拟) “为了安全，请勿超速”．如图，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73）

答案解析收藏纠错 + 选题
22. (2017·盘锦模拟) 某商场有A，B两种商品，若买2件A商品和1件B商品，共需80元；若买3件A商品和2件B商品，共需135元．
1. （1）设A，B两种商品每件售价分别为a元、b元，求a、b的值；
2. （2） B商品每件的成本是20元，根据市场调查：若按（1）中求出的单价销售，该商场每天销售B商品100件；若销售单价每上涨1元，B商品每天的销售量就减少5件．
  ①求每天B商品的销售利润y（元）与销售单价（x）元之间的函数关系？
  ②求销售单价为多少元时，B商品每天的销售利润最大，最大利润是多少？
答案解析收藏纠错 + 选题
23. (2017·安顺模拟) 如图，AB是⊙O的直径，点C是⊙O上一点，∠BAC的平分线AD交⊙O于点D，过点D垂直于AC的直线交AC的延长线于点E．
1. （1）求证：DE是⊙O的切线；
2. （2）如果AD=5，AE=4，求AC长．
答案解析收藏纠错 + 选题
24.
如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
1. （1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
2. （2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
3. （3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．
答案解析收藏纠错 + 选题