浙江省杭州市西湖区2019届九年级上学期数学期末考试试卷

更新时间：2019-12-25 浏览次数：657 类型：期末考试

一、单选题

1. (2018九上·西湖期末) 已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·扬州模拟) 如图，点A，B，P是⊙O上的三点，若 $\text{[math]}$ ，则∠APB的度数为（）

A . 80° B . 140° C . 20° D . 50°

答案解析收藏纠错 + 选题
3. (2019九上·太原月考) 下列每个选项中的两个图形一定相似的是（）

A . 任意两个矩形 B . 两个边长不等的正五边形 C . 任意两个平行四边形 D . 两个等腰三角形

答案解析收藏纠错 + 选题
4. (2018九上·西湖期末)
在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球为白球的概率是 $\text{[math]}$ ，则黄球的个数为（　　）.

A . 16 B . 12 C . 8 D . 4

答案解析收藏纠错 + 选题
5. (2020九上·安庆月考) 将二次函数y＝5x²的图象先向右平移2个单位，再向下平移3个单位，得到的函数图象的解析式为（）

A . y＝5（x+2）²+3 B . y＝5（x﹣2）²+3 C . y＝5（x+2）²﹣3 D . y＝5（x﹣2）²﹣3

答案解析收藏纠错 + 选题
6. (2018九上·西湖期末) 如图，正方形OABC的边长为8，点P在AB上，CP交OB于点Q ．若S_△_BPQ＝ $\text{[math]}$ ，则OQ长为（）

A . 6 B . 6 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2018九上·西湖期末) 一元二次方程x²+bx+c=0有一个根为x=3，则二次函数y=2x²﹣bx﹣c的图象必过点（）

A . （﹣3，0） B . （3，0） C . （﹣3，27） D . （3，27）

答案解析收藏纠错 + 选题
8. (2018九上·西湖期末) 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分是∠BAC，∠EAD，若DE=6，∠BAC+∠EAD=180°，则圆心A到弦BC的距离等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 3

答案解析收藏纠错 + 选题
9. (2018九上·西湖期末) 对于代数式ax²+bx+c(a≠0)，下列说法正确的是（）
①如果存在两个实数p≠q，使得ap²+bp+c=aq²+bq+c，则a $\text{[math]}$ +bx+c=a（x-p）（x-q）②存在三个实数m≠n≠s，使得am²+bm+c=an²+bn+c=as²+bs+c③如果ac＜0，则一定存在两个实数m＜n，使am²+bm+c＜0＜an²+bn+c④如果ac＞0，则一定存在两个实数m＜n，使am²+bm+c＜0＜an²+bn+c

A . ③ B . ①③ C . ②④ D . ①③④

答案解析收藏纠错 + 选题
10. (2018九上·西湖期末) 在数学拓展课《折叠矩形纸片》上，小林发现折叠矩形纸片ABCD可以进行如下操作：①把△ABF翻折，点B落在C边上的点E处，折痕为AF ，点F在BC边上；②把△ADH翻折，点D落在AE边上的点G处，折痕为AH ，点H在CD边上，若AD＝6，CD＝10，则 $\text{[math]}$ ＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·余杭月考) 抛物线y＝2x²﹣2x与x轴的交点坐标为．

答案解析收藏纠错 + 选题
12. (2020九上·北仑期末) 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使一次拨对的概率小于 $\text{[math]}$ ，则密码的位数至少要设置位．

答案解析收藏纠错 + 选题
13. (2022八下·龙凤期中) 把10cm长的线段进行黄金分割后得两条线段，其中较长的线段的长为cm ．

答案解析收藏纠错 + 选题
14. (2022·广东模拟) 如图，平行四边形ABCD中，点E是AD边上一点，连结EC、BD交于点F ，若AE：ED＝5：4记△DFE的面积为S₁ ， △BCF的面积为S₂ ， △DCF的面积为S₃ ，则DF：BF＝，S₁：S₂：S₃＝．

答案解析收藏纠错 + 选题
15. (2023九上·上杭期中) 已知抛物线y＝﹣x²﹣3x+3，点P（m ， n）在抛物线上，则m+n的最大值是．

答案解析收藏纠错 + 选题

三、解答题

16. (2018九上·西湖期末) 求半径为3的圆的内接正方形的边长．

答案解析收藏纠错 + 选题
17. (2019九上·寻乌月考) 在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x ，再从乙袋中随机抽取一个小球，记录标有的数字为y ，确定点M坐标为（x ， y）．
1. （1）用树状图或列表法列举点M所有可能的坐标；
2. （2）求点M（x ， y）在函数y＝﹣x+1的图象上的概率．
答案解析收藏纠错 + 选题
18. (2018九上·西湖期末) 如图，在△ABC中，AD⊥BC ， AD²＝BD•CD ，记△ADB的面积为S_△_ADB ， △CDA的面积为S_△_CDA ．
1. （1）求证：△ADB∽△CDA；
2. （2）若S_△_ADB：S_△_CDA＝1：4，求tanB ．
答案解析收藏纠错 + 选题
19. (2018九上·西湖期末) 已知二次函数y＝ax²+bx+c中，函数y与自变量x的部分对应值如表：

x

…

﹣1

0

1

2

3

…

y

…

10

5

2

1

2

…
1. （1）当x＝4时，求y的值；
2. （2）当y＜10时，求x的取值范围．
答案解析收藏纠错 + 选题
20. (2018九上·西湖期末) 如图，已知△ABC中，AB＝BC ， AC＝2，cosA＝ $\text{[math]}$ ．
1. （1）求BC与BC边上高的长；
2. （2）设边BC的垂直平分线与边AB的交点为D ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2018九上·西湖期末) 已知两个函数：y₁＝ax+4，y₂＝a（x﹣ $\text{[math]}$ ）（x﹣4）（a≠0）．
1. （1）求证：y₁的图象经过点M（0，4）；
2. （2）当a＞0，﹣2≤x≤2时，若y＝y₂﹣y₁的最大值为4，求a的值；
3. （3）当a＞0，x＜2时，比较函数值y₁与y₂的大小．
答案解析收藏纠错 + 选题
22. (2018九上·西湖期末) 如图所示，在△ABC中，AB＝AC＝5，O为BC边中点，BC＝8，点E、G是线段AB上的动点（不与端点重合），点H、F是线段AC上的动点，且EF∥GH∥BC ．设点O到EF、GH的距离分别为x、y ．
1. （1）若△EOF的面积为S：
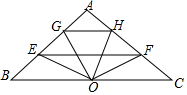
  ①用关于x的代数式表示线段EF的长；
  
  ②求S的最大值；
2. （2）以点O为圆心，当以OE为半径的圆与以OG为半径的圆重合时，求x与y应满足的关系式，并求x的取值范围．
答案解析收藏纠错 + 选题