2017年安徽省蚌埠市高考数学二模试卷（理科）

更新时间：2024-07-12 浏览次数：791 类型：高考模拟

一、选择题：

1. (2017高二下·莆田期末) 已知集合A={x|x²﹣2x≤0}，B={﹣1，0，1，2}，则A∩B=（）

A . [0，2] B . {0，1，2} C . （﹣1，2） D . {﹣1，0，1}

答案解析收藏纠错 + 选题
2. (2017·蚌埠模拟) 已知复数z满足iz=1﹣i，则 $\text{[math]}$ =（）

A . ﹣1﹣i B . 1﹣i C . ﹣1+i D . 1+i

答案解析收藏纠错 + 选题
3. (2017·襄阳模拟) 函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2017·蚌埠模拟) 已知等差数列{a_n}的前n项和为S_n ，且S₆=24，S₉=63，则a₄=（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
5. (2017·蚌埠模拟) 如图所示的程序框图中，如输入m=4，t=3，则输出y=（）

A . 61 B . 62 C . 183 D . 184

答案解析收藏纠错 + 选题
6. (2017·蚌埠模拟) 平行四边形ABCD中，AB=2，AD=1， $\text{[math]}$ • $\text{[math]}$ =﹣1，点M在边CD上，则 $\text{[math]}$ • $\text{[math]}$ 的最大值为（）

A . 2 B . 2 $\text{[math]}$ ﹣1 C . 5 D . $\text{[math]}$ ﹣1

答案解析收藏纠错 + 选题
7. (2017·蚌埠模拟) 在射击训练中，某战士射击了两次，设命题p是“第一次射击击中目标”，命题q是“第二次射击击中目标”，则命题“两次射击中至少有一次没有击中目标“为真命题的充要条件是（）

A . （￢p）∨（￢q）为真命题 B . p∨（￢q）为真命题 C . （￢p）∧（￢q）为真命题 D . p∨q为真命题

答案解析收藏纠错 + 选题
8. (2017·蚌埠模拟) 已知双曲线 $\text{[math]}$ ，以原点O为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A，B，C，D四点，这四点围成的四边形面积为b，则双曲线的离心率为（）

A . $\text{[math]}$ B . 2 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017高一下·新余期末) 已知函数f（x）=cos² $\text{[math]}$ + $\text{[math]}$ sinωx﹣ $\text{[math]}$ （ω＞0），x∈R，若f（x）在区间（π，2π）内没有零点，则ω的取值范围是（）

A . （0， $\text{[math]}$ ] B . （0， $\text{[math]}$ ]∪[ $\text{[math]}$ ， $\text{[math]}$ ） C . （0， $\text{[math]}$ ] D . （0， $\text{[math]}$ ]∪[ $\text{[math]}$ ， $\text{[math]}$ ]

答案解析收藏纠错 + 选题
10. (2017·蚌埠模拟) 已知函数f（x）=x（a﹣ $\text{[math]}$ ），曲线y=f（x）上存在两个不同点，使得曲线在这两点处的切线都与y轴垂直，则实数a的取值范围是（）

A . （﹣e² ， +∞） B . （﹣e² ， 0） C . （﹣ $\text{[math]}$ ，+∞） D . （﹣ $\text{[math]}$ ，0）

答案解析收藏纠错 + 选题
11. (2017·蚌埠模拟) 如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该几何体的体积为（）

A . 15 B . 16 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2017·蚌埠模拟) 数列{a_n}是以a为首项，q为公比的等比数列，数列{b_n}满足b_n=1+a₁+a₂+…+a_n（n=1，2，…），数列{c_n}满足c_n=2+b₁+b₂+…+b_n（n=1，2，…）．若{c_n}为等比数列，则a+q=（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题

二、填空题：

13. (2017·蚌埠模拟) 二项式（ $\text{[math]}$ ﹣ $\text{[math]}$ ）ⁿ的展开式中，所有项的二项式系数之和为4096，则常数项等于．

答案解析收藏纠错 + 选题
14. (2017·蚌埠模拟) 已知边长为 $\text{[math]}$ 的正△ABC的三个顶点都在球O的表面上，且OA与平面ABC所成的角为60^° ，则球O的表面积为．

答案解析收藏纠错 + 选题
15. (2017·蚌埠模拟) 过O点作直线l的垂线所得的垂足称为点P在直线l上的射影，由区域 $\text{[math]}$ 内的点在直线l：λ（2x﹣3y﹣9）+μ（x+y﹣2）=0上的射影构成线段记为MN，则|MN|的长度的最大值为．

答案解析收藏纠错 + 选题
16. (2017·蚌埠模拟) 赌博有陷阱．某种赌博游戏每局的规则是：参与者现在从标有5、6、7、8、9的相同小球中随机摸取一个，将小球上的数字作为其赌金（单位：元）；随后放回该小球，再随机摸取两个小球，将两个小球上数字之差的绝对值的2倍作为其资金（单位：元）．若随机变量ξ和η分别表示参与者在每一局赌博游戏中的赌金与资金，则E_ξ﹣E_η=（元）．

答案解析收藏纠错 + 选题

三、解答题：

17. (2017·蚌埠模拟) 在△ABC中，内角A，B，C所对的边分别为a，b，c，已知2sin2A+sin（A﹣B）=sinC，且 $\text{[math]}$ ．
（Ⅰ）求 $\text{[math]}$ 的值；
（Ⅱ）若c=2， $\text{[math]}$ ，求△ABC的面积．

答案解析收藏纠错 + 选题
18. (2017·蚌埠模拟) 如图，四棱锥P﹣ABCD中，平面PAC⊥平面ABCD，AC=2BC=2CD=4，∠ACB=∠ACD=60°．
1. （1）证明：CP⊥BD；
2. （2）若AP=PC=2 $\text{[math]}$ ，求二面角A﹣BP﹣C的余弦值．
答案解析收藏纠错 + 选题
19. (2017·蚌埠模拟) 某学校高一、高二、高三三个年级共有300名教师，为调查他们的备课时间情况，通过分层抽样获得了20名教师一周的备课时间，数据如下表（单位：小时）：
高一年级
7
7.5
8
8.5
9
高二年级
7
8
9
10
11
12
13
高三年级
6
6.5
7
8.5
11
13.5
17
18.5
1. （1）试估计该校高三年级的教师人数；
2. （2）从高一年级和高二年级抽出的教师中，各随机选取一人，高一年级选出的人记为甲，高二年级选出的人记为乙，假设所有教师的备课时间相对独立，求该周甲的备课时间不比乙的备课时间长的概率；
3. （3）再从高一、高二、高三三个年级中各随机抽取一名教师，他们该周的备课时间分别是8、9、10（单位：小时），这三个数据与表格中的数据构成的新样本的平均数记为 $\text{[math]}$ ，表格中的数据平均数记为 $\text{[math]}$ ，试判断 $\text{[math]}$ 与 $\text{[math]}$ 的大小．（结论不要求证明）
答案解析收藏纠错 + 选题
20. (2017·新余模拟)
如图，已知椭圆 $\text{[math]}$ （a＞b＞0）的左右顶点分别是A（﹣ $\text{[math]}$ ，0），B（ $\text{[math]}$ ，0），离心率为 $\text{[math]}$ ．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点是O．

（Ⅰ）证明：OP⊥BC；
（Ⅱ）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．

答案解析收藏纠错 + 选题
21. (2017·蚌埠模拟) 已知函数f（x）=ax²+（1﹣2a）x﹣lnx（a∈R）．
1. （1）求函数f（x）在区间[1，2]上的最大值；
2. （2）若A（x₁ ， y₁），B（x₂ ， y₂），C（x₀ ， y₀）是函数f（x）图象上不同的三点，且x₀= $\text{[math]}$ ，试判断f′（x₀）与 $\text{[math]}$ 之间的大小关系，并证明．
答案解析收藏纠错 + 选题
22. (2017·蚌埠模拟) 在极坐标系中，曲线C₁：ρ=2cosθ，曲线C₂：ρ=（ρ•cosθ+4）•cosθ．以极点为坐标原点，极轴为x轴正半轴建立直角坐标系xOy，曲线C的参数方程为 $\text{[math]}$ （t为参数）．
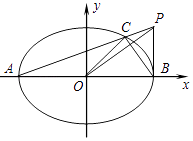
（Ⅰ）求C₁ ， C₂的直角坐标方程；
（Ⅱ）C与C₁ ， C₂交于不同四点，这四点在C上的排列顺次为H，I，J，K，求||HI|﹣|JK||的值．

答案解析收藏纠错 + 选题
23. (2017·成都模拟) 已知x，y∈R，m+n=7，f（x）=|x﹣1|﹣|x+1|．
1. （1）解不等式f（x）≥（m+n）x；
2. （2）设max{a，b}= $\text{[math]}$ ，求F=max{|x²﹣4y+m|，|y²﹣2x+n|}的最小值．
答案解析收藏纠错 + 选题