 B .
B . 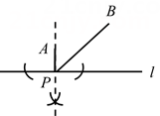 C .
C .  D .
D . 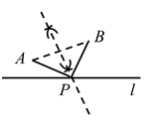
如图是3×4正方形网格,其中已有5各小方格涂上阴影,若再选取标有①,②,③,④中的一个小方格涂上阴影,使图中所有涂上阴影的小方格组成一个中心对称图形,则该小方格是.(填序号)

品种 | 购买个数 | 单价 | 总价 |
甲种足球 |
| ||
乙种足球 | x | 1200 |
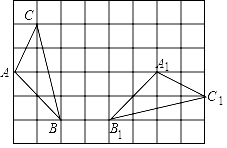
课堂上,老师给出了如下一道探究题:“如图,在边长为1的正方形组成的6×8的方格中,△ABC和△A1B1C1的顶点都在格点上,且△ABC≌△A1B1C1 . 请利用平移或旋转变换,设计一种方案,使得△ABC通过一次或两次变换后与△A1B1C1完全重合.”
甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.

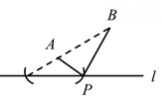
请完善下面证明思路:①先根据 ,证明BM=
DG;②再证明
,得到DG=AC;所以BM=
AC;
拓展延伸:如图3,已知等腰△ABC和等腰△ADE,AB=AC,AD=AE.连接BE,CD,若P是CD的中点,探索:当∠BAC与∠DAE满足什么条件时,AP= BE,并简要说明证明思路.
