吉林省辽源市2018-2019学年九年级上学期数学期末考试试...

更新时间：2024-07-13 浏览次数：235 类型：期末考试

一、单选题

1. (2019九上·辽源期末) 下列图案均是名车的标志，在这些图案中，是中心对称图形的有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2019九上·辽源期末) 已知反比例函数y= $\text{[math]}$ （k≠0）的图象经过点M（-2，2），则k的值是（）

A . -4 B . -1 C . 1 D . 4

答案解析收藏纠错 + 选题
3. (2019九上·辽源期末) 抛物线y=x²+2x+3的对称轴是（）

A . 直线x=1 B . 直线x=﹣1 C . 直线x=﹣2 D . 直线x=2

答案解析收藏纠错 + 选题
4. (2020九上·五莲期末) 在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为（　　）

A . 10m B . 12m C . 15m D . 40m

答案解析收藏纠错 + 选题
5. (2019·零陵模拟) “同吋掷两枚质地均匀的骰子，至少有一枚骰子的点数是3”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019九上·辽源期末) 如图，把直角△ABC的斜边AC放在直线l上，按顺时针的方向在直线l上转动两次，使它转到△A₂B₁C₂的位置，设AB＝ $\text{[math]}$ ，∠BAC＝30°，则顶点A运动到点A₂的位置时，点A所经过的路线为（　　）

A . （ $\text{[math]}$ + $\text{[math]}$ ）π B . （ $\text{[math]}$ + $\text{[math]}$ ）π C . 2π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题

二、填空题

7. (2018九上·营口期末) 已知点P（a+1，1）关于原点的对称点在第四象限，则a的取值范围是．

答案解析收藏纠错 + 选题
8. (2019九上·辽源期末) 若一元二次方程ax²﹣bx﹣2018＝0有一个根为x＝﹣1，则a+b＝．

答案解析收藏纠错 + 选题
9. (2021九上·扶风期末) 若关于 $\text{[math]}$ 的一元二次方程(m-1)x²-4x+1=0有两个不相等的实数根，则m的取值范围为．

答案解析收藏纠错 + 选题
10. (2019九上·辽源期末) 已知抛物线y＝﹣2（x﹣1）²+3，当x时，y随x的增大而减小．

答案解析收藏纠错 + 选题
11. (2022·温州模拟) 已知圆锥的底面圆半径为3，母线长为5，则圆锥的侧面积是.

答案解析收藏纠错 + 选题
12. (2019九上·辽源期末) 如图，边长为6cm的正三角形内接于⊙O，则阴影部分的面积为（结果保留π）．

答案解析收藏纠错 + 选题
13. (2019九上·辽源期末) 如图，矩形ABOC的面积为3，反比例函数y＝ $\text{[math]}$ 的图象过点A ，则k＝（　　）

A . 3 B . ﹣1.5 C . ﹣3 D . ﹣6

答案解析收藏纠错 + 选题
14. (2019九上·辽源期末) 如图，在平面直角坐标系中，点A在抛物线y＝x²﹣2x+2上运动．过点A作AC⊥x轴于点C ，以AC为对角线作矩形ABCD ，连结BD ，则对角线BD的最小值为．

答案解析收藏纠错 + 选题
15. (2019九上·辽源期末) 下面是“作出弧AB所在的圆”的尺规作图过程．
已知：弧AB．

求作：弧AB所在的圆．

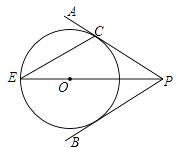
作法：如图，

⑴在弧AB上任取三个点D，C，E；

⑵连接DC，EC；

⑶分别作DC和EC的垂直平分线，两垂直平分线的交点为点O．

⑷以 O为圆心，OC长为半径作圆，所以⊙O即为所求作的弧AB所在的圆．

请回答：该尺规作图的依据是．

答案解析收藏纠错 + 选题

三、解答题

16. (2019九上·辽源期末) 用公式法解方程：3x²﹣6x+1＝2．

答案解析收藏纠错 + 选题
17. (2023九下·睢宁开学考) 一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出一个球是红球的概率为 $\text{[math]}$ .
1. （1）求口袋中黄球的个数；
2. （2）甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用“树状图法”或“列表法”，求两次摸出都是红球的概率；
答案解析收藏纠错 + 选题
18. (2021九上·绥滨期末) 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．
1. （1）求每个月生产成本的下降率；
2. （2）请你预测4月份该公司的生产成本．
答案解析收藏纠错 + 选题
19. (2019九上·辽源期末) 如图是由边长为1的小正方形组成的8×4网格，

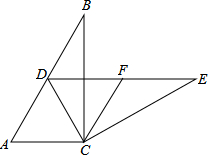
每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：

第一步：点D绕点A顺时针旋转180°得到点D₁；

第二步：点D₁绕点B顺时针旋转90°得到点D₂；

第三步：点D₂绕点C顺时针旋转90°回到点D．
1. （1）请用圆规画出点D→D₁→D₂→D经过的路径；
2. （2）所画图形是什么对称图形；
3. （3）求所画图形的周长（结果保留π）．
答案解析收藏纠错 + 选题
20. (2019九上·辽源期末) 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m ．
1. （1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（）（填方案一，方案二，或方案三），则B点坐标是（），求出你所选方案中的抛物线的表达式；
2. （2）因为上游水库泄洪，水面宽度变为6m ，求水面上涨的高度．
答案解析收藏纠错 + 选题
21. (2019九上·辽源期末) 如图，

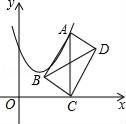
在平面直角坐标系xOy中，一次函数y₁=ax+b（a，b为常数，且a≠0）与反比例函数y₂= $\text{[math]}$ （m为常数，且m≠0）的图象交于点A（﹣2，1）、B（1，n）
1. （1）求反比例函数与一次函数的解析式；
2. （2）连接OA、OB，求△AOB的面积；
3. （3）直接写出当y₁＜y₂时，自变量x的取值范围．
答案解析收藏纠错 + 选题
22. (2019九上·辽源期末) 如图，点O在∠APB的平分线上，⊙O与PA相切于点C．
1. （1）求证：直线PB与⊙O相切；
2. （2） PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．
答案解析收藏纠错 + 选题
23. (2024九上·乐昌期末) 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC，点D刚好落在AB边上．
1. （1）求n的值；
2. （2）若F是DE的中点，判断四边形ACFD的形状，并说明理由．
答案解析收藏纠错 + 选题
24. (2019九上·辽源期末) 结果如此巧合!
下面是小颖对一道题目的解答．

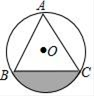
题目：如图，

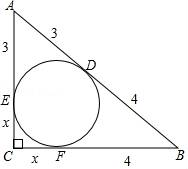
Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．

解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．

根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．

根据勾股定理，得（x+3）²+（x+4）²=（3+4）² ．

整理，得x²+7x=12．

所以S_△_ABC= $\text{[math]}$ AC $\text{[math]}$ BC

= $\text{[math]}$ （x+3）（x+4）

= $\text{[math]}$ （x²+7x+12）

= $\text{[math]}$ ×（12+12）

=12．

小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？

请你帮她完成下面的探索．

已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．

可以一般化吗？
1. （1）若∠C=90°，求证：△ABC的面积等于mn．
2. （2）若AC $\text{[math]}$ BC=2mn，求证∠C=90°．
3. （3）若∠C=60°，用m、n表示△ABC的面积．
答案解析收藏纠错 + 选题
25. (2019九上·辽源期末) 如图，在△ABC中，∠A＝30°，∠C＝90°，AB＝12，四边形EFPQ是矩形，点P与点C重合，点Q、E、F分别在BC、AB、AC上（点E与点A、点B均不重合）．
1. （1）当AE＝8时，求EF的长；
2. （2）设AE＝x，矩形EFPQ的面积为y．
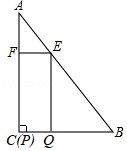
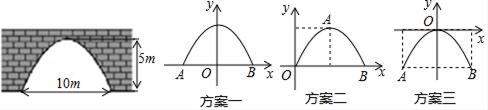
  ①求y与x的函数关系式；
  
  ②当x为何值时，y有最大值，最大值是多少？
3. （3）当矩形EFPQ的面积最大时，将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动（当点P到达点B时停止运动），设运动时间为t秒，矩形EFPQ与△ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．
答案解析收藏纠错 + 选题
26. 如图，在平面直角坐标系中，平行四边形ABOC如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′．抛物线y＝﹣x²+2x+3经过点A、C、A′三点．
1. （1）求A、A′、C三点的坐标；
2. （2）求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积；
3. （3）点M是第一象限内抛物线上的一动点，问点M在何处时，△AMA′的面积最大？最大面积是多少？并写出此时M的坐标．
答案解析收藏纠错 + 选题