云南省晋宁县二街中学2019年数学中考模拟试卷（6月）

更新时间：2024-07-31 浏览次数：236 类型：中考模拟

一、单选题

1. (2020九下·云梦期中) – $\text{[math]}$ 的倒数是（）

A . –5 B . 5 C . – $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·黄冈模拟) 下列立体图形中，主视图是三角形的是（）。

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021·开江模拟) 下列计算正确的是（）

A . 2a+3b＝5ab B . $\text{[math]}$ ＝±6 C . a²b÷2ab＝ $\text{[math]}$ a² D . （2ab²）³＝8a³b⁶

答案解析收藏纠错 + 选题
4. (2022·楚雄模拟) 一组数据：1，3，3，5，若添加一个数据3，则下列统计量中发生变化的是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
5. (2019·晋宁模拟) 函数 $\text{[math]}$ 图象的顶点坐标是（）.

A . （2，-1） B . （2，1） C . （-2，-1） D . （-2，1）

答案解析收藏纠错 + 选题
6. (2019七上·中期中) 国家主席习近平提出“金山银山，不如绿水青山”，国家环保部大力治理环境污染，空气质量明显好转，将惠及13.75亿中国人，这个数字用科学记数法表示为（）

A . 13.75×10⁶ B . 13.75×10⁵ C . 1.375×10⁸ D . 1.375×10⁹

答案解析收藏纠错 + 选题
7. (2019·晋宁模拟) 在△ABC中，已知AB＝AC，sinA＝ $\text{[math]}$ ，则tanB的值是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019·晋宁模拟) 若一次函数y＝kx+b图象经过第一、三、四象限，则关于x的方程x²﹣2x+kb+1＝0的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 只有一个实数根

答案解析收藏纠错 + 选题
9. (2018八下·太原期中) 如图，直线y＝ax+b与x轴交于点A（7，0），与直线y＝kx交于点B（2，4），则不等式kx≤ax+b的解集为（）

A . x≤2 B . x≥2 C . 0＜x≤2 D . 2≤x≤6

答案解析收藏纠错 + 选题
10. (2019·晋宁模拟) 如图，△ABC的两条内角平分线BD与CD交于点D，设∠A的度数为x，∠BDC的度数为y，则y关于x的函数图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2019·上饶模拟) 化简 $\text{[math]}$ 的结果为.

答案解析收藏纠错 + 选题
12. (2019·晋宁模拟) 合肥市初中毕业学业体育考试项目分必考项1项和选考项2项，在8个选考项目中，张明同学可在立定跳远、跳绳和坐位体前屈三个项目模考中基本拿满分，现计划从这三个项目中任选两项作为中考选考项，则跳绳能被选上的概率为.

答案解析收藏纠错 + 选题
13. (2019·晋宁模拟) 已知抛物线y＝x²+bx﹣3（b是常数）经过点A（﹣1，0），（1）求抛物线的解析式.（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P′，当点P′落在第二象限内，P′A²取得最小值时，求m的值.

答案解析收藏纠错 + 选题
14. (2019·晋宁模拟) 如图，在矩形ABCD中，AB=8，将矩形绕点A逆时针旋转90°，到达AB′C′D′的位置，则在旋转过程中，边CD扫过的面积是

答案解析收藏纠错 + 选题
15. (2019·晋宁模拟) 如图，一等腰三角形，底边长是21厘米，底边上的高是21厘米，现在沿底边依次从下往上画宽度均为3厘米的矩形，画出的矩形是正方形时停止，则这个矩形是第个.

答案解析收藏纠错 + 选题

三、解答题

16. (2023八上·应城期末) 先化简，再求值： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ，其中a=2．

答案解析收藏纠错 + 选题

17. (2019·晋宁模拟) 某校有学生3600人，在“文明我先行”的活动中，开设了“法律、礼仪、环保、感恩、互助”五门校本课程，规定每位学生必须且只能选一门，为了解学生的报名意向，学校随机调查了一些学生，并制成统计表和统计图：

课程类别	频数	频率
法律	36	0.09
礼仪	55	0.1375
环保	m	a
感恩	130	0.325
互助	49	0.1225
合计	n	1.00

（1）在这次调查活动中，学校采取的调查方式是（填写“普查”或“抽样调查”）a＝，m＝，n＝.
（2）请补全条形统计图，如果要画一个“校本课程报名意向扇形统计图”，那么“环保”类校本课程所对应的扇形圆心角应为度；
（3）请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人？

答案解析收藏纠错 + 选题

18. (2019·晋宁模拟) 如图，已知AB是⊙O的直径，弦CD⊥AB于点E，F是弧AD上的一点，AF，CD的延长线相交于点G.
1. （1）若⊙O的半径为3 $\text{[math]}$ ，且∠DFC＝45°，求弦CD的长.
2. （2）求证：∠AFC＝∠DFG.
答案解析收藏纠错 + 选题
19. (2019·晋宁模拟) 如图，一次函数的图象与x轴、y轴分别交于A、C两点，与反比例函数的图象交于B点，B点在第四象限，BD垂直平分OA，垂足为D，OB＝ $\text{[math]}$ ，OA＝BD.
1. （1）求该一次函数和反比例函数的解析式；
2. （2）延长BO交反比例函数的图象于点E，连接ED、EC，求四边形BCED的面积.
答案解析收藏纠错 + 选题
20. (2020·郑州模拟) 4月18日，一年一度的“风筝节”活动在市政广场举行，如图，广场上有一风筝A，小江抓着风筝线的一端站在D处，他从牵引端E测得风筝A的仰角为67°，同一时刻小芸在附近一座距地面30米高(BC＝30米)的居民楼顶B处测得风筝A的仰角是45°，已知小江与居民楼的距离CD＝40米，牵引端距地面高度DE＝1.5米，根据以上条件计算风筝距地面的高度(结果精确到0.1米，参考数据：sin67°≈ $\text{[math]}$ ，cos67°≈ $\text{[math]}$ ，tan67°≈ $\text{[math]}$ ， $\text{[math]}$ ≈1.414).

答案解析收藏纠错 + 选题
21. (2019·晋宁模拟) 某电视台摄制组乘船往返于A码头和B码头进行拍摄，在A、B两码头间设置拍摄中心C.在往返过程中，假设船在A、B、C处均不停留，船离开B码头的距离s（千米）与航行的时间t（小时）之间的函数关系式如图所示.根据图象信息，解答下列问题：
1. （1）求船从B码头返回A码头时的速度及返回时s关于t的函数表达式.
2. （2）求水流的速度.
3. （3）若拍摄中心C设在离A码头12千米处，摄制组在拍摄中心分两组拍摄，其中一组乘橡皮艇漂流到B码头处，另一组同时乘船到达A码头后马上返回，求两摄制组相遇时离拍摄中心C的距离.
答案解析收藏纠错 + 选题
22. (2020九上·罗庄期中) 已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE ，连接DE ．
1. （1）如图1，求证：△CDE是等边三角形．
2. （2）设OD＝t ，
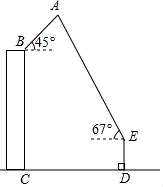
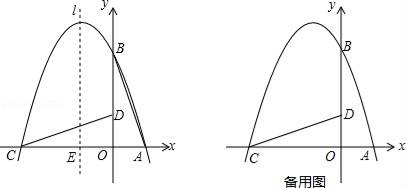
  ①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．
  
  ②求t为何值时，△DEB是直角三角形（直接写出结果即可）．
答案解析收藏纠错 + 选题
23. (2020九上·罗山期末) 如图，在平面直角坐标系中有一直角三角形AOB，O为坐标原点，OA＝1，tan∠BAO＝3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y＝ax²+bx+c经过点A、B、C．
1. （1）求抛物线的解析式；
2. （2）若点P是第二象限内抛物线上的动点，其横坐标为t，设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求以C、E、F为顶点三角形与△COD相似时点P的坐标．
答案解析收藏纠错 + 选题