2017年江苏省镇江市润州区中考数学二模试卷

更新时间：2017-08-10 浏览次数：1226 类型：中考模拟

一、填空题

1. (2017·润州模拟) ﹣ $\text{[math]}$ 的倒数是

答案解析收藏纠错 + 选题
2. (2024七下·綦江期末) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
3. (2017·润州模拟) 分解因式：2x²﹣12x+18=．

答案解析收藏纠错 + 选题
4. (2022·南岗模拟) 函数y= $\text{[math]}$ 中，自变量x的取值范围是．

答案解析收藏纠错 + 选题
5. (2024八上·长沙月考) 若一个多边形的内角和等于720°，则这个多边形是边形．

答案解析收藏纠错 + 选题
6. (2017·润州模拟) 若关于x的一元二次方程kx²+2x﹣1=0有两个实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
7. (2017·润州模拟) △ABC中，D、E分别在AB、AC上，DE∥BC，AD=1，BD=3，则△ADE与△ABC的面积之比为．

答案解析收藏纠错 + 选题
8. (2017·润州模拟) 如图，四边形ABCD是⊙O的内接四边形，∠B=148°24′，则∠AOC的角度为．

答案解析收藏纠错 + 选题
9. (2017·润州模拟) 如图，PA、PB切⊙O于点A、B，已知⊙O半径为2，且∠APB=60°，则AB=．

答案解析收藏纠错 + 选题
10. (2017·润州模拟) 圆锥底面圆的半径为3，高长为4，它的表面积等于（结果保留π）．

答案解析收藏纠错 + 选题
11. (2017·润州模拟)
如图，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A、B两点，D、E分别是AB，OA上的动点，当△CDE周长最小时，点D坐标为．

答案解析收藏纠错 + 选题
12. (2017·邗江模拟) 抛物线y=ax²+bx+3（a≠0）过A（4，4），B （2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是．

答案解析收藏纠错 + 选题

二、选择题

13. (2020九下·合肥月考)
如图是一些完全相同的小正方体搭成的几何体的三视图．这个几何体只能是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
14. (2017·润州模拟) 如图，数轴上的四个点A、B、C、D位置如图所示，它们分别对应四个实数a、b、c、d，若a+c=0，AB＜BC，则下列各式正确的是（）

A . bc＞0 B . b﹣d＞0 C . b+c＞0 D . |a|＞|d|

答案解析收藏纠错 + 选题
15. (2017·润州模拟) 如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，顶点C的坐标为（﹣ $\text{[math]}$ ，3），反比例函数y= $\text{[math]}$ 的图象与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（）

A . 4 $\text{[math]}$ B . ﹣4 $\text{[math]}$ C . 2 $\text{[math]}$ D . ﹣2 $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2017·润州模拟) 已知二次函数y=ax²+bx+c，函数y与自变量x的部分对应值如下表：
x
…
﹣4
﹣3
﹣2
﹣1
0
…
y
…
3
﹣2
﹣5
﹣6
﹣5
…
则下列判断中正确的是（）

A . 抛物线开口向下 B . 抛物线与y轴交于正半轴 C . 方程ax²+bx+c=0的正根在1与2之间 D . 当x=﹣3时的函数值比x=1.5时的函数值大

答案解析收藏纠错 + 选题
17. (2017·润州模拟) 如图，正六边形A₁B₁C₁D₁E₁F₁的边长为2，正六边形A₂B₂C₂D₂E₂F₂的外接圆与正六边形A₁B₁C₁D₁E₁F₁的各边相切，正六边形A₃B₃C₃D₃E₃F₃的外接圆与正六边形A₂B₂C₂D₂E₂F₂的各边相切，…按这样的规律进行下去，A₁₀B₁₀C₁₀D₁₀E₁₀F₁₀的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

18. (2017·润州模拟) 化简求值
1. （1）计算： $\text{[math]}$ ﹣3tan²30°+2 $\text{[math]}$
2. （2）化简： $\text{[math]}$ ÷（1+ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
19. (2017·润州模拟) 解方程
1. （1）解方程： $\text{[math]}$ + $\text{[math]}$ =4
2. （2）解不等式组 $\text{[math]}$ ，并把它们的解集在数轴上表示出来．
答案解析收藏纠错 + 选题
20. (2017·润州模拟)
王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：
1. （1）根据图中提供的数据列出如下统计表：
  
  平均成绩（分）
  中位数（分）
  众数（分）
  方差（S²）
  王华
      80
      b
     80
      d
  张伟
       a
      85
      c
     260
  则a=，b=，c=，d=，
2. （2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是．
3. （3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？
答案解析收藏纠错 + 选题
21. (2017·润州模拟) 如图，在△ABC和△BCD中，AB=DC，AC=DB，AC、DB交于点M．
1. （1）求证：△ABC≌△DCB；
2. （2）作CN∥BD，BN∥AC，CN交BN于点N，求证：四边形BNCM是菱形．
答案解析收藏纠错 + 选题
22. (2021九上·碑林月考) 小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．
1. （1）如果小明第一题不使用“求助”，那么小明答对第一道题的概率是．
2. （2）如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．
3. （3）从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）
答案解析收藏纠错 + 选题
23. (2017·润州模拟)
如图，已知△ABC的三个顶点的坐标分别为A（﹣2，2）、B（﹣5，0）、C（﹣1，0），P（a，b）是△ABC的边AC上一点：
1. （1）将△ABC绕原点O逆时针旋转90°得到△A₁B₁C₁ ，请在网格中画出△A₁B₁C₁ ，旋转过程中点A所走的路径长为 $\text{[math]}$ ．
2. （2）将△ABC沿一定的方向平移后，点P的对应点为P₂（a+6，b+2），请在网格画出上述平移后的△A₂B₂C₂ ，并写出点A₂的坐标：A₂（）．
3. （3）若以点O为位似中心，作△A₃B₃C₃与△ABC成2：1的位似，则与点P对应的点P₃位似坐标为（直接写出结果）．
答案解析收藏纠错 + 选题
24. (2017·润州模拟) 如图，一次函数y₁=k₁x+b与反比例函数y₂= $\text{[math]}$ 的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C．
1. （1） m=，k₁=；
2. （2）当x的取值是时，k₁x+b＞ $\text{[math]}$ ；
3. （3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S_四边形_ODAC：S_△_ODE=3：1时，求点P的坐标．
答案解析收藏纠错 + 选题
25. (2017·润州模拟)
如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离AB=1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离CD=1.5m，看旗杆顶部M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．请求出旗杆MN的高度．（参考数据： $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7，结果保留整数）

答案解析收藏纠错 + 选题
26. (2017·润州模拟) 如图，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，且∠AEC=∠ODB．
1. （1）判断直线BD和⊙O的位置关系，并给出证明；
2. （2）当tan∠AEC= $\text{[math]}$ ，BC=8时，求OD的长．
答案解析收藏纠错 + 选题
27. (2017·润州模拟)
已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．
1. （1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系：．
2. （2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．
3. （3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．
答案解析收藏纠错 + 选题
28. (2017·润州模拟) 已知抛物线y=x²+bx+c的顶点为P，与y轴交于点A，与直线OP交于点B．
1. （1）
  如图1，若点P的横坐标为1，点B的坐标为（3，6），试确定抛物线的解析式；
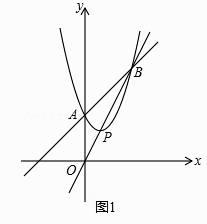
2. （2）在（1）的条件下，若点M是直线AB下方抛物线上的一点，且S_△_ABM=3，求点M的坐标；
3. （3）
  如图2，若点P在第一象限，且PA=PO，过点P作PD⊥x轴于点D．将抛物线y=x²+bx+c平移，平移后的抛物线经过点A、D，该抛物线与x轴的另一个交点为C，请探究四边形OABC的形状，并说明理由．
答案解析收藏纠错 + 选题