 B .
B .  C .
C .  .
D .
.
D . 

 B .
B .  C .
C .  D .
D . 

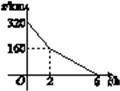

方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
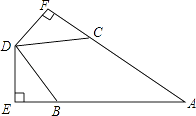
如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC.现将△ABC与△DEF按如图所示的方式叠放在一起,现将△ABC保持不动, △DEF运动,且满足点E在BC边从B向C移动(不与B、C重合),DE始终经过点A,EF与AC边交于点M.求证:△ABE∽△ECM.

