浙江省绍兴市2019-2020学年九年级下学期数学教学质量检...

更新时间：2020-04-23 浏览次数：288 类型：中考模拟

一、选择题（本大题有10小题，每小题4分，共40分.）

1. (2023九上·新北月考) 若小王沿坡度i=3：4的斜坡向上行走10m，则他所在的位置比原来的位置升高了（）

A . 3m B . 4m C . 6m D . 8m

答案解析收藏纠错 + 选题
2. (2020·绍兴模拟) 如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②.关于平移前后几何体的三视图，下列说法正确的是（）

A . 主视图相同 B . 左视图相同 C . 俯视图相同 D . 三种视图均不同

答案解析收藏纠错 + 选题
3. (2023九上·宁强期末) 按如图所示的运算程序，能使输出的y值为 $\text{[math]}$ 的是（）

A . α=60°，β=45° B . α=30°，β=45° C . α=30°，β=30° D . α=45°，β=30°

答案解析收藏纠错 + 选题
4. (2020·绍兴模拟) 如图，AB为 $\text{[math]}$ O的切线，切点为A.连结AO，BO，BO与 $\text{[math]}$ O交于点C，延长BO与 $\text{[math]}$ O交于点D，连结AD.若∠ABO=36°，则∠ADC的度数为（）

A . 27° B . 32° C . 36° D . 54°

答案解析收藏纠错 + 选题
5. (2020·绍兴模拟) 如图，已知 $\text{[math]}$ O的半径为5，直线EF经过 $\text{[math]}$ O上一点P（点E，F在点P的两旁），下列条件能判定直线EF与 $\text{[math]}$ O相切的是（）

A . OP=5 B . OE=OF C . 点O到直线EF的距离是4 D . OP⊥EF

答案解析收藏纠错 + 选题
6. (2020·绍兴模拟) 如图，直线PA、PB、MN分别与 $\text{[math]}$ O相切于点A，B，D，PA=PB=8cm，则△PMN的周长为（）

A . 8cm B . $\text{[math]}$ cm C . 16cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
7. (2020·绍兴模拟) 如图，O为圆锥的顶点，M为圆锥底面上一点，点P在OM上，一只蜗牛从点P出发，绕圆锥侧面沿最短路线爬行一圈回到点P，若沿OM将圆锥侧面剪开并展开，则所得的侧面展开图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2020·绍兴模拟) 如图，AB是 $\text{[math]}$ O的直径，DB、DE分别切 $\text{[math]}$ O于点B、C，若∠ACE=20°，则∠D的度数是（）

A . 40° B . 50° C . 60° D . 70°

答案解析收藏纠错 + 选题
9. (2020·绍兴模拟) 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于（）

A . asinx+bsinx B . acosx+bsinx C . asinx+bcosx D . acosx+bcosx

答案解析收藏纠错 + 选题
10. (2020·绍兴模拟) 如图，有一内部装有水的直圆柱形水桶，桶高20dm；另有一直圆柱形的实心铁柱，柱高30dm，直立放置于水桶底面上，水桶内的水面高度为12dm，且水桶与铁柱的底面半径比为2：1.今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为（）

A . 4.5dm B . 6dm C . 8dm D . 9dm

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题5分，共30分）

11. (2020九下·镇江月考) 如图，在△ABC中，sinB= $\text{[math]}$ ，tanC= $\text{[math]}$ ，AB=3，则AC的长为 .

答案解析收藏纠错 + 选题
12. (2020·绍兴模拟) 如图，∠MAN=60°，若△ABC的顶点B在射线AM上，且AB=2，点C在射线AN上运动，当△ABC是锐角三角形时，BC的取值范围是.

答案解析收藏纠错 + 选题
13. (2020·绍兴模拟) 已知等边三角形ABC的边长为3，则它的内切圆半径为.

答案解析收藏纠错 + 选题
14. (2020·绍兴模拟) 如图所示，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，若以点C为圆心，r为半径的圆与边AB所在直线有公共点，则r的取值范围为.

答案解析收藏纠错 + 选题
15. (2024九下·香洲月考) 如图是由6个形状、大小完全相同的菱形组成的网格，菱形的顶点称为格点.已知菱形的一个角（∠O）为60°，点A，B，C都在格点上，则sin∠ABC的值是..

答案解析收藏纠错 + 选题
16. (2020·绍兴模拟) 已知直线m与半径为10cm的 $\text{[math]}$ O相切于点P，AB是 $\text{[math]}$ O的一条弦，且 $\text{[math]}$ = $\text{[math]}$ ，若AB=12cm，则直线m与弦AB之间的距离为.

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分.）

17. (2020·绍兴模拟) 计算： $\text{[math]}$ -3sin60°-cos30°+2tan45°．

答案解析收藏纠错 + 选题
18. (2020·绍兴模拟) 如图，在离铁塔150m的A处，用测倾仪测得塔顶的仰角为30°12'，测倾仪高AD为1.52m.求铁塔的高BC.（精确到0.1m）
（参考数据：sin30°12'≈0.5030，cos30°12'≈0.8643，tan30°12'≈0.5820）

答案解析收藏纠错 + 选题
19. (2020·绍兴模拟) 如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点A（0，4）、B（-4，4）、C（-6，2），若该圆弧所在圆的圆心为D点，请你利用网格图回答下列问题：
1. （1）圆心D的坐标为；
2. （2）若扇形ADC是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）.
答案解析收藏纠错 + 选题
20. (2020·绍兴模拟) 如图，在10×6的正方形网格中，每个小正方形的边长均为1，线段AB、线段EF的端点均在小正方形的顶点上.

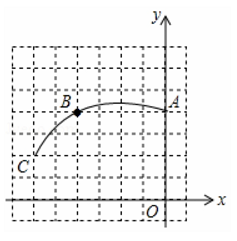
①在图中以AB为边画Rt△ABC，使点C在小正方形的顶点上，且∠BAC=90°，tan∠ACB= $\text{[math]}$ ；

②在①的条件下，在图中画以EF为边且面积为3的△DEF，使点D在小正方形的顶点上，且∠CBD=45°，连结CD，直接写出线段CD的长.

答案解析收藏纠错 + 选题
21. (2021九上·平阴期末) 如图，在△ABC中，AB=AC，∠BAC=120°，点D在BC边上， $\text{[math]}$ D经过点A和点B且与BC边相交于点E.
1. （1）求证：AC是 $\text{[math]}$ D的切线.
2. （2）若CE= $\text{[math]}$ ，求 $\text{[math]}$ D的半径.
答案解析收藏纠错 + 选题
22. (2020九下·江阴期中) 小明家的门框上装有一把防盗门锁（如图1），其平面结构图如图2所示，锁身可以看成由两条等弧 $\text{[math]}$ ， $\text{[math]}$ 和矩形ABCD组成的， $\text{[math]}$ 的圆心是倒锁按钮点M.已知 $\text{[math]}$ 的弓形高GH=2cm，AD=8cm，EP=11cm.当锁柄PN绕着点N顺时针旋转至NQ位置时，门锁打开，此时直线PQ与 $\text{[math]}$ 所在的圆相切，且PQ∥DN，tan∠NQP=2.
1. （1）求 $\text{[math]}$ 所在圆的半径；
2. （2）求线段AB的长度.（ $\text{[math]}$ ≈2.236，结果精确到0.1cm）
答案解析收藏纠错 + 选题
23. (2020·绍兴模拟) 如图，在△ABC中，BA=BC，以AB为直径的 $\text{[math]}$ O分别交AC，BC于点D，E，BC的延长线与 $\text{[math]}$ O的切线AF交于点F.
1. （1）求证：∠ABC=2∠CAF.
2. （2）若AC= $\text{[math]}$ ，CE：EB=1：4，求CE的长.
答案解析收藏纠错 + 选题
24. (2020·绍兴模拟) 如图，已知直线l：y=- $\text{[math]}$ x+8交x轴于点E，点A为x轴上的一个动点（点A不与点E重合），在直线l上取一点B（点B在x轴上方），使BE=5AE，连结AB，以AB为边在AB的右侧作正方形ABCD，连结OB，以OB为直径作 $\text{[math]}$ P.
1. （1）当点A在点E左侧时，若点B落在y轴上，则AE的长为，点D的坐标为.
2. （2）若 $\text{[math]}$ P与正方形ABCD的边相切于点B，求点B的坐标；
3. （3） $\text{[math]}$ P与直线BE的交点为Q，连结CQ，当CQ平分∠BCD时，BE的长为.（直接写出答案）
答案解析收藏纠错 + 选题