河北省遵化市2020年中考数学二模考试试卷

更新时间：2024-11-06 浏览次数：418 类型：中考模拟

一、选择题（本大题共16个小题，共42分，1~10小题，每小题3分；11~16小题，每小题2分。）

1. (2020·遵化模拟) - $\text{[math]}$ =（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八上·衡阳月考) 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）

A . 1 B . 2 C . 8 D . 11

答案解析收藏纠错 + 选题
3. (2020·遵化模拟)
用八根木条钉成如图所示的八边形木架，要使它不变形，至少要钉上木条的根数是（　　）

A . 3根 B . 4根 C . 5根 D . 6根

答案解析收藏纠错 + 选题
4. (2020·遵化模拟) 由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图所示，则小正方体的个数不可能是（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
5. (2020·遵化模拟) 55万用科学记数法表示为（）

A . 5.5×10⁶ B . 5.5×10⁵ C . 5.5×10⁴ D . 5.5×10³

答案解析收藏纠错 + 选题
6. (2020·遵化模拟) 关于 $\text{[math]}$ 的叙述正确的是（）

A . $\text{[math]}$ B . 在数轴上不存在表示 $\text{[math]}$ 的点 C . $\text{[math]}$ =±2 $\text{[math]}$ D . 与 $\text{[math]}$ 最接近的整数是3

答案解析收藏纠错 + 选题
7. (2019八下·仙桃期末) 如表是某公司员工月收入的资料．
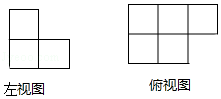
月收入/元
45000
18000
10000
5500
5000
3400
3300
1000
人数
1
1
1
3
6
1
11
1
能够反映该公司全体员工月收入水平的统计量是（）

A . 平均数和众数 B . 平均数和中位数 C . 中位数和众数 D . 平均数和方差

答案解析收藏纠错 + 选题
8. (2020·遵化模拟) 如图，三角形纸片 $\text{[math]}$ ， $\text{[math]}$ ，点E为AB的中点.沿过点E的直线折叠，使点B与点A重合，折痕EF交BC于点F.已知 $\text{[math]}$ ，则BC的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·遵化模拟) 已知： $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . -3

答案解析收藏纠错 + 选题
10. (2020·遵化模拟) 如图在△ABC中，DE∥BC，EF∥AB，要判定四边形DBFE是菱形，还需要添加的条件是（）

A . AB=AC B . AD=BD C . BE⊥AC D . BE平分∠ABC

答案解析收藏纠错 + 选题
11. (2024七下·市中区期中) 若 $\text{[math]}$ ，则x，y的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023八上·鸠江月考) 下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）

A . 甲和乙 B . 乙和丙 C . 甲和丙 D . 只有丙

答案解析收藏纠错 + 选题
13. (2020·遵化模拟) 已知a ， b是有理数，则a² -2a+4的最小值是（）

A . 3 B . 5 C . 6 D . 8

答案解析收藏纠错 + 选题
14. (2020·遵化模拟) 已知二次函数y＝－x²－4x－5，左、右平移该抛物线，顶点恰好落在正比例函数y＝－x的图象上，则平移后的抛物线的解析式为（）

A . y＝－x²－4x－1 B . y＝－x²－4x－2 C . y＝－x²＋2x－1 D . y＝－x²＋2x－2

答案解析收藏纠错 + 选题
15. (2020·遵化模拟) 如图3，在5×5正方形网格中，一条圆弧经过A ， B ， C三点，那么这条圆弧所在圆的圆心是（）

A . 点P B . 点R C . 点Q D . 点M

答案解析收藏纠错 + 选题
16. (2020·遵化模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，且平分 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题 (本大题有3个小题，共12分，17～18小题各3分；19小题有2个空，每空3分。)

17. 已知a与b的和为2，b与c互为相反数，若 $\text{[math]}$ =1，则a=.

答案解析收藏纠错 + 选题
18. (2020·遵化模拟) 三棱柱的三视图如图所示，已知△EFG中，EF=8cm，EG=12cm，∠EFG=45°．则AB的长为cm．

答案解析收藏纠错 + 选题
19. (2020·遵化模拟) 阅读下文，寻找规律填空：
已知x≠1时，（1-x）（1+x）=1-x² ，（1-x）（1+x+x²）=1-x³ ，（1-x）（1+x+x²+x³）=1-x⁴…
1. （1）（1-x）（）=1-x⁸；
2. （2）观察上式，并猜想：（1-x）（1+x+x²+…+xⁿ）=．
答案解析收藏纠错 + 选题

三、解答题(本大题有7个小题，共66分。)

20. (2020·遵化模拟) 利用平方差公式可以进行简便计算：
例1：99×101=(100-1)(100+1)=100²-1²=10 000-1=9 999；

例2：39×410=39×41×10=(40-1)(40+1)×10=(40²-1²)×10=(1600-1)×10=1599×10=15 990.

请你参考上述算法，运用平方差公式简便计算：
1. （1） $\text{[math]}$ ；
2. （2） (2 019 $\text{[math]}$ +2 019 $\text{[math]}$ )( $\text{[math]}$ - $\text{[math]}$ ).
答案解析收藏纠错 + 选题
21. (2021八下·佳木斯期中) 如图，E是平行四边形ABCD的边CD的中点，延长AE交BC的延长线于点F．
1. （1）求证：△ADE≌△FCE．
2. （2）若∠BAF=90°，BC=5，EF=3，求平行四边形ABCD的面积．
答案解析收藏纠错 + 选题

22. (2020·遵化模拟) 为了发展学生的核心素养，培养学生的综合能力，石家庄某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用下面的折线统计图表示：（甲为实线，乙为虚线）

（1）依据折线统计图，得到下面的表格：

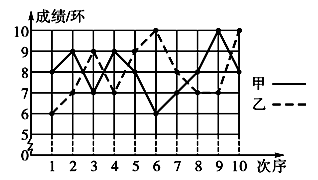
射击次序（次）	1	2	3	4	5	6	7	8	9	10
甲的成绩（环）	8	9	7	9	8	6	7		10	8
乙的成绩（环）	6	7	9	7	9	10	8	7		10

其中，；

（2）甲成绩的众数是环，乙成绩的中位数是环；
（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？
（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率.

答案解析收藏纠错 + 选题

23. (2020·遵化模拟) 机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.（本题参考数据：sin67.4°＝ $\text{[math]}$ ，cos67.4°＝ $\text{[math]}$ ，tan67.4°＝ $\text{[math]}$ ）
1. （1）求弦BC的长；
2. （2）请判断点A和圆的位置关系，试说明理由.
答案解析收藏纠错 + 选题

24. (2020九上·西华期中) 随着地铁和共享单车的发展，“地铁＋单车”已成为很多市民出行的选择．李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家．设他出地铁的站点与文化宫站的距离为 $\text{[math]}$ (单位：km)，乘坐地铁的时间 $\text{[math]}$ (单位：min)是关于 $\text{[math]}$ 的一次函数，其关系如下表：

地铁站	A	B	C	D	E
x/km	7	9	11	12	13
y₁/min	16	20	24	26	28

（1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；
（2）李华骑单车的时间 $\text{[math]}$ (单位：min)也受 $\text{[math]}$ 的影响，其关系可以用 $\text{[math]}$ ＝ $\text{[math]}$ $\text{[math]}$ ²－11 $\text{[math]}$ ＋78来描述．求李华应选择在哪一站出地铁，才能使他从文化宫站回到家所需的时间最短，并求出最短时间．

答案解析收藏纠错 + 选题

25. (2020·遵化模拟) 已知Rt△OAB ， ∠OAB=90^o ， ∠ABO=30^o ，斜边OB=4，将Rt△OAB绕点O顺时针旋转60^o ，如图1，连接BC.
1. （1） ΔOBC的形状是；
2. （2）如图1，连接AC ，作OP⊥AC ，垂足为P ，求OP的长度；
3. （3）如图2，点M、N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒.设运动时间为x秒，△OMN的面积为y ，求当x为何值时y取得最大值？最大值为多少？（结果可保留根号）
答案解析收藏纠错 + 选题
26. (2020·遵化模拟) 如图13-1至图13-5，⊙O均作无滑动滚动，⊙O₁、⊙O₂、⊙O₃、⊙O₄均表示⊙O与线段AB或BC相切于端点时刻的位置，⊙O的周长为c ．
阅读理解：

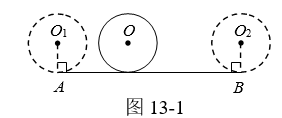
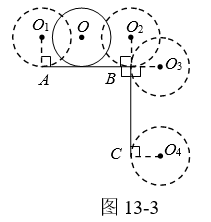
①如图13-1，⊙O从⊙O₁的位置出发，沿AB滚动到⊙O₂的位置，当AB=c时，⊙O恰好自转1周．

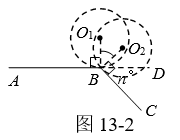
②如图13-2，∠ABC相邻的补角是n°，⊙O在∠ABC外部沿A-B-C滚动，在点B处，必须由⊙O₁的位置旋转到⊙O₂的位置，⊙O绕点B旋转的角∠O₁BO₂ = n°，⊙O在点B处自转 $\text{[math]}$ 周．
1. （1）实践应用：
  在阅读理解的①中，若AB = 2c ，则⊙O自转周；若AB=1 ，则⊙O自转周．在阅读理解的②中，若∠ABC = 120°，则⊙O在点B处自转周；若∠ABC = 60°，则⊙O在点B处自转周．
2. （2）如图13-3，∠ABC=90°，AB=BC= $\text{[math]}$ c ． ⊙O从⊙O₁的位置出发，在∠ABC外部沿A-B-C滚动到⊙O₄的位置，⊙O自转周．
3. （3）拓展联想：
  如图13-4，△ABC的周长为l ， ⊙O从与AB相切于点D的位置出发，在△ABC外部，按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，⊙O自转了多少周？请说明理由．
4. （4）如图13-5，多边形的周长为l ， ⊙O从与某边相切于点D的位置出发，在多边形外部，按顺时针方向沿多边形滚动，又回到与该边相切于点D的位置，直接写出⊙O自转的周数．
答案解析收藏纠错 + 选题