
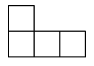
 B .
B . 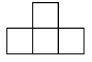 C .
C . 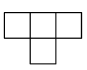 D .
D . 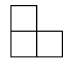


教学方式改进前抽取的学生的成绩在 组中的数据为:80,83,85,87,89.
教学方式改进后抽取的学生成绩为:72,70,76,100,98,100,82,86,95,90,100,86,84,93,88.
教学方式改进前抽取的学生成绩频数分布直方图
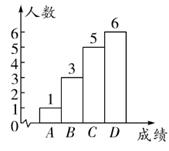
教学方式改进前后抽取的学生成绩对比统计表
| 统计量 | 改进前 | 改进后 |
| 平均数 | 88 | 88 |
| 中位数 | | |
| 众数 | 98 | |
根据以上信息,解答下列问题:
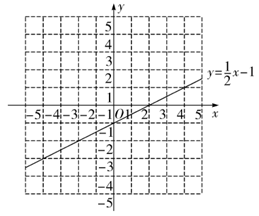
在函数 中,当
时,
;当
时,
.
① 的数量关系是
② 的数量关系是
将图①中 绕点
逆时针旋转
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
将 绕点
旋转任意角度,若
,请直接写出点
在同一直线上时
的长.