
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 561 | 560 | 561 | 560 |
| 方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择.



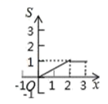 B .
B . 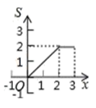 C .
C . 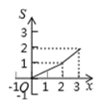 D .
D . 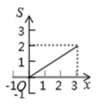




|
2019年中考体育成绩(分数段)统计表 |
||
|
分数段 |
频数(人) |
频率 |
|
25≤x<30 |
12 |
0.05 |
|
30≤x<35 |
24 |
b |
|
35≤x<40 |
60 |
0.25 |
|
40≤x<45 |
a |
0.45 |
|
45≤x<50 |
36 |
0.15 |

根据上面提供的信息,回答下列问题:
已知平面内两点P1(x1 , y1),P2(x2 , y2),其两点间的距离 。例如:已知P(3,1),Q(1,-2),则这两点间的距离
.特别地,如果两点M(x1 , y1),N(x2 , y2),所在的直线与坐标轴重合或平行于坐标轴或者垂直于坐标轴,那么这两点间的距离公式可简化为
或
。

|
进价(元/盒) |
售价(元/盒) |
|
|
甲种 |
40 |
48 |
|
乙种 |
106 |
128 |
设该经销离购进甲种包装的苦荞茶x盒,总进价为y元。
(问题情境)
在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。
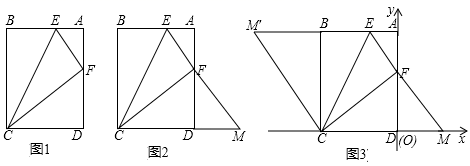
(操作发现)
把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.