重庆市璧山区青杠初级中学校2020年数学中考一模试卷

更新时间：2020-06-12 浏览次数：342 类型：中考模拟

一、选择题

1. (2020七上·河源月考) 比-3大5的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·金牛期末) 如图所示的几何体是由 $\text{[math]}$ 个大小相同的小立方块搭成，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·揭阳模拟) 2019年4月10日，人类首张黑洞图片问世，该黑洞位于室女座一个巨椭圆星系 $\text{[math]}$ 的中心，距离地球 $\text{[math]}$ 万光年.将数据 $\text{[math]}$ 万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·乐亭期中) 在平面直角坐标系中，将点 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位长度后得到的点的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·天元月考) 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·乌鲁木齐模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·松山月考) 分式方程 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·重庆模拟) 如图所示，直线y₁=﹣ $\text{[math]}$ x与双曲线y= $\text{[math]}$ 交于A，B两点，点C在x轴上，连接AC，BC.当AC⊥BC，S_△ABC=15时，求k的值为（　　）

A . ﹣10 B . ﹣9 C . 6 D . 4

答案解析收藏纠错 + 选题
9. (2023九上·安顺期末) 如图，正五边形 $\text{[math]}$ 内接于⊙ $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上的一点（点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合），则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020·重庆模拟) 一天，小战和同学们一起到操场测量学校旗杆高度，他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°，然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°（身高忽略不计）.已知斜坡CD坡度i=1：2.4，坡长为2.6米，旗杆AB所在旗台高度EF为1.4米，旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为（　　）米.
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

A . 10.2 B . 9.8 C . 11.2 D . 10.8

答案解析收藏纠错 + 选题
11. (2020·重庆模拟) 若关于x的分式方程 $\text{[math]}$ ﹣ $\text{[math]}$ =3的解为正整数，且关于y的不等式组 $\text{[math]}$ 至多有六个整数解，则符合条件的所有整数m的取值之和为（　　）

A . 1 B . 0 C . 5 D . 6

答案解析收藏纠错 + 选题
12. (2020·重庆模拟) △ABC中，∠ACB=45°，D为AC上一点，AD=5 $\text{[math]}$ ，连接BD，将△ABD沿BD翻折至△EBD，点A的对应点E点恰好落在边BC上.延长BC至点F，连接DF，若CF=2，tan∠ABD= $\text{[math]}$ ，则DF长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 $\text{[math]}$ D . 7 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2024九下·焦作模拟) 若 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2020·重庆模拟) 如图，在△ABC中，AB=AC，点D，E都在边BC上，∠BAD=∠CAE，若BD=9，则CE的长为.

答案解析收藏纠错 + 选题
15. (2024八下·南明月考) 已知一次函数y＝（k﹣3）x+1的图象经过第一、二、四象限，则k的取值范围是.

答案解析收藏纠错 + 选题
16. (2020·重庆模拟) 如图，平行四边形ABCD的对角线AC与BD相交于点O，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交AO，AB于点M，N；②以点O为圆心，以AM长为半径作弧，交OC于点M'；③以点M'为圆心，以MN长为半径作弧，在∠COB内部交前面的弧于点N'；④过点N'作射线ON'交BC于点E.若AB＝8，则线段OE的长为.

答案解析收藏纠错 + 选题
17. (2020·重庆模拟) A、B两地之间有一修理厂C，一日小海和王陆分别从A、B两地同时出发相向而行，王陆开车，小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行，王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行，王陆到达A地后立即返回B地，到B地后不再继续前行，等待小海前来（装载摩托车时间和掉头时间忽略不计），整个行驶过程中王陆速度不变，而小海在修理厂花了十分钟修好摩托车，为了赶时间，提速 $\text{[math]}$ 前往目的地B，小海到达B地后也结束行程，若图象表示的是小海与王陆二人到修理厂C的距离和y（km）与小海出行时间之间x（h）的关系，则当王陆第二次与小海在行驶中相遇时，小海离目的地B还有km.

答案解析收藏纠错 + 选题
18. (2020·重庆模拟) 如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A'B'D'，分别连接A'C，A'D，B'C，则A'C+B'C的最小值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020·重庆模拟)
1. （1）计算： $\text{[math]}$ .
2. （2）解不等式组： $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2020八下·定远期末) 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理、描述和分析.部分信息如下：
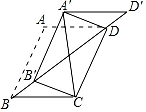
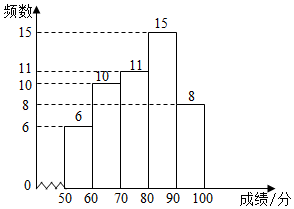
a.七年级成绩频数分布直方图：

b.七年级成绩在 $\text{[math]}$ 这一组的是：70 72 74 75 76 76 77 77 77 78 79

c.七、八年级成绩的平均数、中位数如下：

年级

平均数

中位数

七

76.9

m

八

79.2

79.5

根据以上信息，回答下列问题：
1. （1）在这次测试中，七年级在80分以上（含80分）的有人；
2. （2）表中m的值为；
3. （3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；
4. （4）该校七年级学生有400人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数.
答案解析收藏纠错 + 选题
21. (2022·临邑模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ .
1. （1）求反比例函数的表达式；
2. （2）设一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象的另一个交点为 $\text{[math]}$ ，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
22. (2022·莘县模拟) 甲、乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的 1.5 倍，两人各加工 600 个这种零件，甲比乙少用 5 天．
1. （1）求甲、乙两人每天各加工多少个这种零件？
2. （2）已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元，现有 3000 个这种零件的加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完成．如果总加工费不超过 7800 元，那么甲至少加工了多少天？
答案解析收藏纠错 + 选题
23. (2020·重庆模拟) 模具厂计划生产面积为4，周长为m的矩形模具.对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：
1. （1）建立函数模型
  设矩形相邻两边的长分别为x，y，由矩形的面积为4，得 $\text{[math]}$ ，即 $\text{[math]}$ ；由周长为m，得 $\text{[math]}$ ，即 $\text{[math]}$ .满足要求的 $\text{[math]}$ 应是两个函数图象在第象限内交点的坐标.
2. （2）画出函数图象
  函数 $\text{[math]}$ 的图象如图所示，而函数 $\text{[math]}$ 的图象可由直线 $\text{[math]}$ 平移得到.请在同一直角坐标系中直接画出直线 $\text{[math]}$ .
3. （3）平移直线 $\text{[math]}$ ，观察函数图象
  ①当直线平移到与函数 $\text{[math]}$ 的图象有唯一交点 $\text{[math]}$ 时，求周长m的值；
  
  ②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围.
4. （4）得出结论
  若能生产出面积为4的矩形模具，则周长m的取值范围为.
答案解析收藏纠错 + 选题
24. (2020·重庆模拟) 如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10.
1. （1）在旋转过程中，
  ①当A，D，M三点在同一直线上时，求AM的长.
  
  ②当A，D，M三点为同一直角三角形的顶点时，求AM的长.
2. （2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D₁转到其内的点D₂处，连结D₁D₂ ，如图2，此时∠AD₂C＝135°，CD₂＝60，求BD₂的长.
答案解析收藏纠错 + 选题
25. (2020·平阳模拟) 如图，抛物线y=ax²+bx+c经过点A（﹣2，5），与x轴相交于B（﹣1，0），C（3，0）两点.
1. （1）求抛物线的函数表达式；
2. （2）点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC′D，若点C′恰好落在抛物线的对称轴上，求点C′和点D的坐标；
答案解析收藏纠错 + 选题
26. (2020·重庆模拟) 如图

如图1和图2，在△ABC中，AB＝13，BC＝14， $\text{[math]}$ .
1. （1）探究：如图1，AH⊥BC于点H，则AH＝，AC＝，△ABC的面积 $\text{[math]}$ ＝.
2. （2）拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $\text{[math]}$ ＝0）.
  
  用含x、m或n的代数式表示 $\text{[math]}$ 及 $\text{[math]}$ ；
3. （3）求(m+n)与x的函数关系式，并求(m+n)的最大值和最小值；
4. （4）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
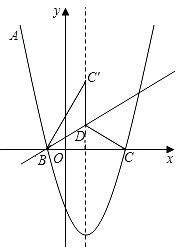
  发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.
答案解析收藏纠错 + 选题