北京市海淀区外国语实验学校2020年中考数学5月模拟试卷

更新时间：2020-06-19 浏览次数：238 类型：中考模拟

一、单选题

1. (2020·海淀模拟) 一个等边三角形在太阳光的照射下，在地面上的投影不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020·海淀模拟) 有A、B两只不透明口袋，每只口袋里装有两只相同的球，A袋中的两只球上分别写了“快”“慢”的字样，B袋中的两只球上分别写了“审”“答”的字样，从每只口袋里各摸出一只球，刚好能组成“慢审”字样的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022八上·长沙期中) 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程378里，第一天健步行走，第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（）

A . 24里 B . 12里 C . 6里 D . 3里

答案解析收藏纠错 + 选题
4. (2020·海淀模拟) 小红不小心把家里的一块圆形玻璃打碎了，需要配制一块同样大小的玻璃镜，工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A，B，C，给出三角形ABC，则这块玻璃镜的圆心是（）

A . AB，AC边上的中线的交点 B . AB，AC边上的垂直平分线的交点 C . AB，AC边上的高所在直线的交点 D . ∠BAC与∠ABC的角平分线的交点

答案解析收藏纠错 + 选题
5. (2020·杭州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以BC的中点O为圆心的 $\text{[math]}$ 分别与AB，AC相切于D，E两点，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·海淀模拟) 如图，抛物线 $\text{[math]}$ 交x轴于点A（a ， 0）和B（b ， 0），交y轴于点C ，抛物线的顶点为D ，下列四个结论：
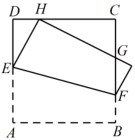
①点C的坐标为（0，m）；

②当m=0时，△ABD是等腰直角三角形；

③若a＝－1，则b＝4；

④抛物线上有两点P（ $\text{[math]}$ ， $\text{[math]}$ ）和Q（ $\text{[math]}$ ， $\text{[math]}$ ），若 $\text{[math]}$ ＜1＜ $\text{[math]}$ ，且 $\text{[math]}$ ＋ $\text{[math]}$ ＞2，则 $\text{[math]}$ ＞ $\text{[math]}$ ．

其中结论正确的序号是（）

A . ①② B . ①②③ C . ①②④ D . ②③④

答案解析收藏纠错 + 选题
7. (2020·海淀模拟) 如图，将正方形 $\text{[math]}$ 折叠，使顶点 $\text{[math]}$ 与 $\text{[math]}$ 边上的一点 $\text{[math]}$ 重合（ $\text{[math]}$ 不与端点 $\text{[math]}$ ， $\text{[math]}$ 重合），折痕交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，边 $\text{[math]}$ 折叠后与边 $\text{[math]}$ 交于点 $\text{[math]}$ ，设正方形 $\text{[math]}$ 的周长为 $\text{[math]}$ ， $\text{[math]}$ 的周长为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. (2020·海淀模拟) 一个大矩形按如图方式分割成九个小矩形，且只有标号为①和②的两个小矩形为正方形，在满足条件的所有分割中，若知道九个小矩形中 n 个小矩形的周长，就一定能算出这个大矩形的面积，则 n 的最小值是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·哈尔滨模拟) 分解因式：2a²+4a+2=．

答案解析收藏纠错 + 选题
10. (2023九上·惠州开学考) 若二次根式 $\text{[math]}$ 有意义，则x的取值范围是

答案解析收藏纠错 + 选题
11. (2020·海淀模拟) 计算 $\text{[math]}$ 的结果是

答案解析收藏纠错 + 选题
12. (2020·海淀模拟) 点 $\text{[math]}$ 是函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象在第一象限内的交点， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2020·海淀模拟) 如图， $\text{[math]}$ 三个顶点的坐标分别为 $\text{[math]}$ ，以原点O为位似中心，把这个三角形缩小为原来的 $\text{[math]}$ ，可以得到 $\text{[math]}$ ，已知点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是.

答案解析收藏纠错 + 选题
14. (2020·海淀模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，弦 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2020·海淀模拟) 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ．如果正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，那么 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的最小距离是 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

16. (2020·海淀模拟) 某校初三年级240名师生参加社会实践活动，计划租车前往，租车收费标准如下：

车型	大巴车（最多可坐 55人）	中巴车（最多可坐 40人）	小巴车（最多可坐 25人）
每车租金（元∕天）	1050	800	550

则租车一天的最低费用为元．

答案解析收藏纠错 + 选题

三、解答题

17. (2020·海淀模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2020·海淀模拟) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2020·海淀模拟) 如图，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2020·海淀模拟) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ．
1. （1）求证：无论 $\text{[math]}$ 取何实数，方程总有两个不相等的实数根；
2. （2）若方程的一个根是3，求 $\text{[math]}$ 的值及方程的另一个根．
答案解析收藏纠错 + 选题
21. (2020·海淀模拟) 如图，菱形ABCD的对角线AC和BD交于点O，分别过点C． D作CE∥BD，DE∥AC，CE和DE交于点E.
1. （1）求证：四边形ODEC是矩形；
2. （2）当∠ADB=60°，AD=2 $\text{[math]}$ 时，求EA的长。
答案解析收藏纠错 + 选题

22. (2020七下·房县期末) 中华文明，源远流长；中华汉字，寓意深广．为了传承优秀传统文化，某校团委组织了一次全校1000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了200名学生的成绩（成绩 $\text{[math]}$ 取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩 $\text{[math]}$ /分	频数	频率
$\text{[math]}$	10	0.05
$\text{[math]}$	20	0.10
$\text{[math]}$	30	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	0.30
$\text{[math]}$	80	0.40

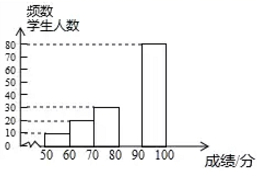
请根据所给的信息，解答下列问题：

（1） $\text{[math]}$ ， $\text{[math]}$ ；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数会落在分数段；
（4）若成绩在90分以上（包括90分）的为优等，则该校参加这次比赛的1000名学生中成绩优等的大约有多少人？

答案解析收藏纠错 + 选题

23. (2020·杭州模拟) 在平面直角坐标系 $\text{[math]}$ 中，A（-4，3），B（0，1），将线段AB沿 $\text{[math]}$ 轴的正方向平移 $\text{[math]}$ 个单位，得到线段A′B′，且A′，B′恰好都落在反比例函数 $\text{[math]}$ 的图象上．
1. （1）用含 $\text{[math]}$ 的代数式表示点A′，B′的坐标；
2. （2）求 $\text{[math]}$ 的值和反比例函数 $\text{[math]}$ 的表达式；
3. （3）点 $\text{[math]}$ 为反比例函数 $\text{[math]}$ 图象上的一个动点，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，请直接写出点C的坐标．
答案解析收藏纠错 + 选题
24. (2020·海淀模拟) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，对角线 $\text{[math]}$ 为 $\text{[math]}$ 的直径，过点 $\text{[math]}$ 作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF．
1. （1）求证：DF是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
25. (2020·海淀模拟) 阅读下面材料：
上课时孙老师提出这样一个问题：对于任意实数 $\text{[math]}$ ，关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的取值范围．

小明的思路是：原不等式等价于 $\text{[math]}$ ，设函数 $\text{[math]}$ ， $\text{[math]}$ ，画出两个函数的图象的示意图，于是原问题转化为函数 $\text{[math]}$ 的图象在 $\text{[math]}$ 的图象上方时 $\text{[math]}$ 的取值范围．

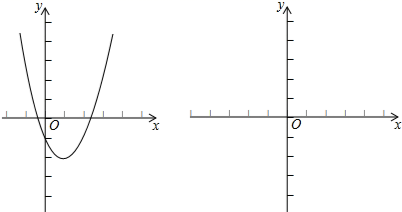
请结合小明的思路回答：
1. （1）对于任意实数 $\text{[math]}$ ，关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 恒成立，则 $\text{[math]}$ 的取值范围是．
2. （2）参考小明思考问题的方法，解决问题：
  关于 $\text{[math]}$ 的方程 $\text{[math]}$ 在 $\text{[math]}$ 范围内有两个解，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
26. (2020·杭州模拟) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于A，B两点（点A在点B左侧）
1. （1）求抛物线的顶点坐标（用含 $\text{[math]}$ 的代数式表示）；
2. （2）求线段AB的长；
3. （3）抛物线与 $\text{[math]}$ 轴交于点C（点C不与原点 $\text{[math]}$ 重合），若 $\text{[math]}$ 的面积始终小于 $\text{[math]}$ 的面积，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2020·海淀模拟)
1. （1）发现
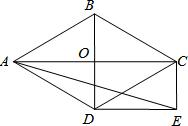
  如图1，点A为线段BC外一动点，且 $\text{[math]}$ ， $\text{[math]}$ ．
  
  填空：当点A位于时，线段AC的长取得最大值，且最大值为．（用含 $\text{[math]}$ ， $\text{[math]}$ 的式子表示）
2. （2）应用
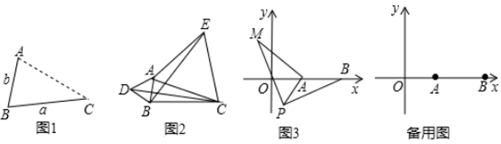
  点A为线段BC外一动点，且 $\text{[math]}$ ， $\text{[math]}$ ．如图2所示，分别以 $\text{[math]}$ ， $\text{[math]}$ 为边，作等边 $\text{[math]}$ 和等边 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
  
  ①请找出图中与 $\text{[math]}$ 相等的线段，并说明理由；
  
  ②直接写出线段 $\text{[math]}$ 长的最大值．
3. （3）拓展
  如图3，在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，点B的坐标为（4，0），点P为线段AB外一动点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．请直接写出线段AM长的最大值及此时点P的坐标．
答案解析收藏纠错 + 选题
28. (2022·济南模拟) 若抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ）与直线 $\text{[math]}$ 都经过 $\text{[math]}$ 轴上的一点 $\text{[math]}$ ，且抛物线 $\text{[math]}$ 的顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，则称此直线 $\text{[math]}$ 与该抛物线 $\text{[math]}$ 具有“一带一路”关系．此时，直线 $\text{[math]}$ 叫做抛物线 $\text{[math]}$ 的“带线”，抛物线 $\text{[math]}$ 叫做直线 $\text{[math]}$ 的“路线”．
1. （1）若直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 具有“一带一路”关系，求 $\text{[math]}$ 的值；
2. （2）若某“路线” $\text{[math]}$ 的顶点在反比例函数 $\text{[math]}$ 的图象上，它的“带线” $\text{[math]}$ 的解析式为 $\text{[math]}$ ，求此“路线” $\text{[math]}$ 的解析式；
3. （3）当常数 $\text{[math]}$ 满足 $\text{[math]}$ 时，请直接写出抛物线 $\text{[math]}$ ： $\text{[math]}$ 的“带线” $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴所围成的三角形面积S的取值范围．
答案解析收藏纠错 + 选题