浙江省瑞安市瑞祥学校2020年数学中考一模试卷

更新时间：2020-06-28 浏览次数：320 类型：中考模拟

一、选择题(共10小题，每小题4分，满分40分，)

1. (2020·瑞安模拟) 计算6×(-9)的结果等于（）

A . -15 B . 15 C . 54 D . -54

答案解析收藏纠错 + 选题
2. (2020·瑞安模拟) 2019年10月1日，在新中国成立70周年的阅兵式上，4名上将，2名中将，100多名少将，近15000名官兵接受祖国和人民的检阅.15000这个数用科学记数法可表示为（）

A . 15×10³ B . 0.15×10⁵ C . 1.5×10⁴ D . 1.5×10³

答案解析收藏纠错 + 选题
3. (2023九下·德化月考) 长方体的主视图、俯视图如图所示，则其左视图面积为（）

A . 3 B . 4 C . 12 D . 16

答案解析收藏纠错 + 选题
4. (2020·瑞安模拟) 某校体育室里有球类数量如表，如果随机拿出一个球(每一个球被拿出来的可能性是一样的)，那么拿出一个球是足球的可能性是（）

球类

篮球

排球

足球

数量

3

5

4

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·瑞安模拟) 为筹备即将举行的校园文化艺术节，九(1)班文体委员对全班50名同学的特长进行了一次调查，并将结果绘制成一幅不完整的扇形统计图，则特长是“诗歌朗诵”的人数有（）

A . 5名 B . 10名 C . 15名 D . 20名

答案解析收藏纠错 + 选题
6. (2020·瑞安模拟) 如图，为了保证道路交通安全，某段高速公路在A处设立观测点，与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒。若∠BAC=α，则此车的速度为（）

A . 5tanα米/秒 B . 80tanα米/秒 C . $\text{[math]}$ 米/秒 D . $\text{[math]}$ 米/秒

答案解析收藏纠错 + 选题
7. (2021九上·谷城期中) 当a-1≤x≤a时，函数y=x²-2x+1的最小值为1，则a的值为（）

A . 1 B . 2 C . 1或2 D . 0或3

答案解析收藏纠错 + 选题
8. (2020·瑞安模拟) 已知：如图，直线1经过点A(-2，0)和点B(0，1)，点M在x轴上，过点M作x轴的垂线交直线l于点C，若OM=2OA，则经过点C的反比例函数表达式为（）

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y= $\text{[math]}$ D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·瑞安模拟) 如图，在扇形OAB中，∠AOB=90°，半径OA=6，将扇形OAB沿过点A的直线折叠，点O恰好落在弧AB上的点O处，折痕交OB于点C，则弧OB的长是（）

A . $\text{[math]}$ π B . Π C . 2π D . 3π

答案解析收藏纠错 + 选题
10. (2020·瑞安模拟) 如图，在正方形ABCD中，边长为a，在边BC、CD上取点E、G，使EC=GC=b，作EF∥AB，FG∥BC两线相交于点F，欧几里得在《几何原本》中利用该图解释了(a+b)(a-b)=a²-b² ，现以点A为圆心，AC为半径作圆弧交线段AD的延长线于点H，连结CH，记图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ，若点B，F，H在同一直线上，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本题有6小题，每小题5分，共30分)

11. (2020·瑞安模拟) 分解因式：m²-9n²= 。

答案解析收藏纠错 + 选题
12. (2020·瑞安模拟) 不等式组 $\text{[math]}$ 的解为。

答案解析收藏纠错 + 选题
13. (2020·瑞安模拟) 某市号召居民节约用水，为了解居民用水情况，随机抽查了20户家庭某月的用水量，结果如友表：则这20户家庭的该月平均用水量为吨。

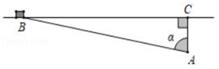
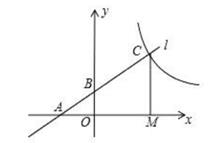
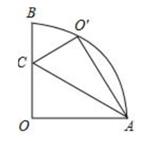
户数

10

6

4

用水量（吨）

4

6

7

答案解析收藏纠错 + 选题
14. (2020·瑞安模拟) 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC。若∠C=20°，则∠A=。

答案解析收藏纠错 + 选题
15. (2020·瑞安模拟) 如图，边长为12的正方形ABCD中点E、F分别在AB、BC上，F是BC的中点且DF⊥EF，则线段DE的长为。

答案解析收藏纠错 + 选题
16. (2020·瑞安模拟) 图1是小红在“淘宝·双11”活动中所购买的一张多档位可调节靠椅，档位调节示意图如图2所示。已知两支脚AB=AC，为AC上固定连接点，靠背OD=10分米。档位为Ⅰ档时，OD∥AB，档位为Ⅱ挡时，OD’⊥AC。当靠椅由Ⅰ档调节为Ⅱ档时，靠背顶端D向后靠至D’，此时点D移动的水平距离是2分米，即ED’=2分米。DE⊥BC交OD’于点G，则DG=分米。

答案解析收藏纠错 + 选题

三、解答题(本题有8小题，共80分。解答需写出必要的文字说明、演算步骤或证明过程)

17. (2020·瑞安模拟) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020·瑞安模拟) 如图，在四边形ABCD中，AB∥CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．
1. （1）求证：△ABE≌△CDF；
2. （2）若AC与BD交于点O，求证：AC与BD互相平分．
答案解析收藏纠错 + 选题
19. (2020·瑞安模拟) 某公司销售部有营业员16人，销售部为了制定某种商品的月销售定额，统计了这16人某月的销售量如下：

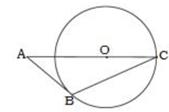
每人销售件数

10

11

12

13

14

15

人数

1

3

4

3

3

2
1. （1）这16位销售员该月销售量的众数是，中位数是,平均数是.
2. （2）若要使75%的营业员都能完成任务，应选什么统计量（平均数、中位数和众数）作为月销售件数的定额？请说明理由.
答案解析收藏纠错 + 选题
20. (2020·瑞安模拟) 如图，在8×5的方格中有线段AD，作三边互不相等的△ABC，使其满足下列条件：
1. （1）在图甲中，作格点Rt△ABC，使AD为△ABC的中线。
2. （2）在图乙中，作格点△ABC，使AD为△ABC的高线。
答案解析收藏纠错 + 选题
21. (2020·瑞安模拟) 如图，抛物线y=ax²+bx过点B(1，-3)，对称轴是直线x=2，且抛物线与x轴的正半轴交于点A。
1. （1）求抛物线的解析式，并根据图象直接写出当y≤0时，自变量x的取值范围；
2. （2）在第二象限内的抛物线上有一点P，当PA⊥BA时，求△PAB的面积。
答案解析收藏纠错 + 选题
22. (2020·瑞安模拟) 如图，直线DP和⊙O相切于点C，交直线AE的延长线于点P，过点C作AE的垂线，交AE于点F，交⊙O于点B，作平行四边形ABCD，连结BE，DO，CO。
1. （1）求证：DA=DC。
2. （2）求∠P及∠AEB的大小。
答案解析收藏纠错 + 选题
23. (2020·瑞安模拟) 王主任到文具批发市场购买甲、乙两种笔记本当期末学生奖品，已知甲种笔记本每本13元，乙种笔记本每本10元。
1. （1）王主任用560元购买两种笔记本共50本，问购买甲、乙两种笔记本各多少本？
2. （2）若王主任用680元购买甲、乙两种笔记本，且甲种笔记本比乙种笔记本至少多1本，那么他最多购买乙种笔记本多少本？
3. （3）为增加奖品种类，王主任共买了甲、乙、丙三种笔记本，已知丙种笔记本每本6元，丙种笔记本的数量是甲、乙两种笔记本数量的和，他一共用了216元，请求出所有满足条件的购买方案。
答案解析收藏纠错 + 选题
24. (2020·瑞安模拟) 如图所示，直线y= $\text{[math]}$ x+6分别与x轴，y轴交于A，B两点，直线y=x与AB交于点C，与过点A且平行于y轴的直线交于点D，点P从A点出发，以1个单位每秒的速度沿x轴向左运动，过点P作x轴的垂线，分别交直线AB，OD于E、F两点，以EF为边向右做正方形EFGH。设正方形EFGH与△ACD重叠阴影部分的面积为S(平方单位)，点P的运动时间为t秒。
1. （1） ①则点C的坐标为。
  ②当0≤t<4.8时，s关于t的函数关系式；
  
  当4.8≤t≤8时，s关于t的函数关系式。
2. （2）当(1)②条件中S取最大值的时候，求tan∠EOF值。
3. （3）当t>0时，如果△CEF与△CEO相似，求t的值。
4. （4）当t>0时，直接写出点(6，4)在正方形内部(包括边上)时，t的取值范围。
答案解析收藏纠错 + 选题