吉林省四平市公主岭市2019-2020学年七年级下学期数学期...

更新时间：2020-07-02 浏览次数：255 类型：期中考试

一、单选题

1. (2024八上·秦安月考) 4的算术平方根是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020七下·吉林期中) 在实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，无理数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2020七下·吉林期中) 如图，数轴上点P表示的数一定不可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020七下·潢川期中) 如图，在一次活动中，位于 $\text{[math]}$ 处的七年一班准备前往相距 $\text{[math]}$ 的 $\text{[math]}$ 处与七年二班会合，若用方向和距离描述七年二班相对于七年一班的位置，可以描述为（）

A . 南偏西40°，3km B . 南偏西50°，3km C . 北偏东40°，3km D . 北偏东50°，3km

答案解析收藏纠错 + 选题
5. (2020七下·吉林期中) 下列各图中，∠1和∠2是对顶角的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2020七下·吉林期中) 下列命题中，是真命题的是（）

A . 互补的角是邻补角 B . 相等的角是对顶角 C . 同旁内角互补 D . 两直线平行，内错角相等

答案解析收藏纠错 + 选题
7. (2021八下·滦南期中) 如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点（-1，-2），“馬”位于点（2，-2），则“兵”位于点（）

A . （-2，3） B . （-2，1） C . （-3，1） D . （-3，3）

答案解析收藏纠错 + 选题
8. (2020七下·吉林期中) 已知a，b，c是三条直线，下列结论正确的是（）

A . 若a∥b，b∥c，则a∥c B . 若a⊥b，b⊥c，则a⊥c C . 若a∥b，b⊥c，则a∥c D . 若a⊥b，b∥c，则a∥c

答案解析收藏纠错 + 选题

二、填空题

9. (2020七下·吉林期中) 若 $\text{[math]}$ 有意义，则a的值为（写出一个即可）．

答案解析收藏纠错 + 选题
10. (2020七下·吉林期中) 若一个正数的两个平方根分别为 $\text{[math]}$ 和 $\text{[math]}$ ，则x的值为．

答案解析收藏纠错 + 选题
11. (2022七下·梅里斯期末) 如图，要在河的两岸搭建一座桥，在PA，PB，PC三种搭建方式中，最短的是PB，其理由是．

答案解析收藏纠错 + 选题
12. (2022七下·舒兰期末) 如图，直线AB，CD被直线EF所截，如果∠2=100°，那么∠1的同位角等于度．

答案解析收藏纠错 + 选题
13. (2020七下·吉林期中) 若点P（x+1，x-3）在x轴上，则x的值为．

答案解析收藏纠错 + 选题
14. (2020七下·吉林期中) 如图，三角形ABC中任意一点P（x，y），经过平移后对应点为P₁（x+5，y-1），将三角形ABC作同样的平移得到三角形A₁B₁C₁ ，若点A的坐标为（-4，5），则点A₁的坐标为．

答案解析收藏纠错 + 选题
15. (2020七下·吉林期中) 请完成下面的解答过程．
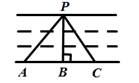
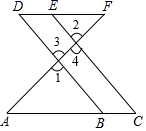
如图，∠1=∠B，∠C=110°，求∠3的度数．

解：∵∠1=∠B，

∴AD∥（）

∴∠C+=180°．（两直线平行，同旁内角互补）

∵∠C=110°，

∴∠2=°．

∴∠3==70°．（）

答案解析收藏纠错 + 选题

三、解答题

16. (2020七下·吉林期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2020七下·吉林期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2020七下·吉林期中) 如图，将三角形ABC向下平移3个单位长度，可以得到三角形A₁B₁C₁ ．
1. （1）在坐标系中画出平移后的三角形A₁B₁C₁；
2. （2）点B₁的坐标为；
3. （3）线段AA₁的长度为个单位长度．
答案解析收藏纠错 + 选题
19. (2020七下·贵州月考) 如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．试说明：AC∥DF．

答案解析收藏纠错 + 选题
20. (2020七下·潢川期中) 如图①，将两个边长为1的小正方形分别沿对角线剪开，拼成正方形ABCD．
1. （1）正方形ABCD的面积为，边长为，对角线BD=；
2. （2）求证： $\text{[math]}$ ；
3. （3）如图②，将正方形ABCD放在数轴上，使点B与原点O重合，边AB落在x轴的负半轴上，则点A所表示的数为，若点E所表示的数为整数，则点E所表示的数为
答案解析收藏纠错 + 选题
21. (2020七下·潢川期中) 如图，直线AB，CD相交于点O，OM⊥AB．
1. （1） ∠AOC的邻补角为（写出一个即可）；
2. （2）若∠1=∠2，判断ON与CD的位置关系，并说明理由；
3. （3）若∠1= $\text{[math]}$ ∠BOC，求∠MOD的度数．
答案解析收藏纠错 + 选题
22. (2020七下·吉林期中) 如图，在长方形OABC中，O为平面直角坐标系的原点，点A，点C分别在x轴，y轴上，点B坐标为（4，6），点P从点O出发，以每秒2个单位长度的速度沿O→C→B方向运动，到点B停止．设点P运动的时间为t（秒）．
1. （1）点A的坐标为；
2. （2）当t=1秒时，点P的坐标；
3. （3）当点P在OC上运动，请直接写出点P的坐标（用含有t的式子表示）；
4. （4）在移动过程中，当点P到y轴的距离为1个单位长度时，求t的值．
答案解析收藏纠错 + 选题
23. (2020七下·吉林期中) 如图，将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置，连接AC'．
1. （1） AA'与CC'的位置关系为；
2. （2）求证：∠A'+∠CAC'+∠AC'C=180°；
3. （3）设 $\text{[math]}$ ∠ACB=y，试探索∠CAC'与x，y之间的数量关系，并证明你的结论．
答案解析收藏纠错 + 选题
24. (2020七下·吉林期中) 问题情境：
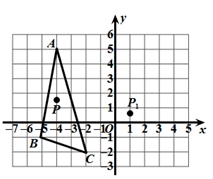
如图，在平面直角坐标系中有三点A（x₁ ， y₁），B（x₂ ， y₂），C（x₃ ， y₃），小明在学习中发现，当x₁=x₂ ， AB∥y轴，线段AB的长度为|y₁﹣y₂|；当y₁=y₃ ， AC∥x轴，线段AC的长度为|x₁﹣x₃|．
1. （1）初步应用
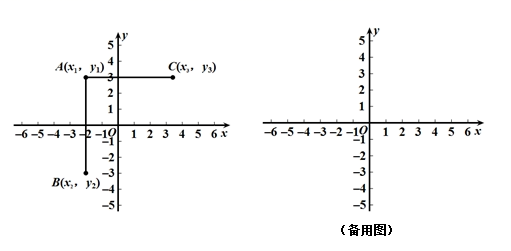
  若点A（﹣1，1）、B（2，1），则AB∥轴（填“x”或“y”）；
2. （2）若点C（1，﹣2），CD∥y轴，且点D在x轴上，则CD=；
3. （3）若点E（﹣3，2），点F（t，﹣4），且EF∥y轴，t=；
4. （4）拓展探索：
  已知P（3，﹣3），PQ∥y轴．
  
  若三角形OPQ的面积为3，求满足条件的点Q的坐标．
5. （5）若PQ=a，将点Q向右平移b个单位长度到达点M，已知点M在第一象限角平分线上，请直接写出a，b之间满足的关系．
答案解析收藏纠错 + 选题