| 甲 | 乙 | 丙 | 丁 | |
| 平均数（cm） | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
根据表数据，从中选择一名成绩好且发挥稳定的参加比赛，应该选择（ ）
| 步数（万步） | 1.0 | 1.2 | 1.1 | 1.4 | 1.3 |
| 天数 | 3 | 3 | 5 | 7 | 12 |
在每天所走的步数这组数据中，众数和中位数分别是（ ）
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 
表示弹簧的初始长度，用厘米（cm）表示，K表示单位重力物体作用在弹簧上时弹簧的长度，用厘米（cm）表示．下面给出的四个公式中，表明这是一个短而硬的弹簧的是（ ）
①当 时，两个探测气球位于同一高度
②当 时，乙气球位置高；
③当 时，甲气球位置高；
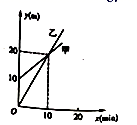
其中，符合题意结论的个数是（ ）
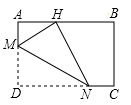
宽与长的比是 （约为0.618）的矩形叫做黄金矩形，黄金矩形给我们以协调，匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果，都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.（提示； MN=2）
第一步，在矩形纸片一端.利用图①的方法折出一个正方形，然后把纸片展平.
第二步，如图②.把这个正方形折成两个相等的矩形，再把纸片展平.
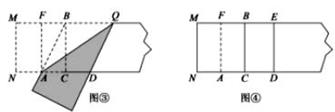
第三步，折出内侧矩形的对角线 AB，并把 AB折到图③中所示的AD处，
第四步，展平纸片，按照所得的点D折出DE，使DE⊥ND，则图④中就会出现黄金矩形，
问题解决：
①求线段 的长；
②在 轴上，是否存在点
，使得
为等腰三角形？若存在，请直接写出符合条件的所有点
的坐标；若不存在，请说明理由．
