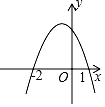一、选择题(本大题有10小题,每小题4分,共40分.)
-
A . 0
B . 2
C . ﹣3
D . ﹣ 
-
2.
(2020·云南模拟)
近期,新型冠状病毒感染肺炎的疫情在全国蔓延,全国人民团结一致,全力抗击新型冠状病毒感染肺炎.多国政府官员及机构高度赞赏并支持中国政府抗击疫情的有力措施,表示对中国早日战胜疫情充满信心,社会各界人士积极捐款.截止2月5日中午12点,武汉市慈善总会接收捐赠款约3230000000元.14亿中国人民众志成城、行动起来、战斗起来,一定能打赢这场疫情防控阻击战,将3230000000用科学记数法表示应为( )
A . 323×107
B . 32.3×108
C . 3.23×109
D . 3.23×1010
-
A . ①③②
B . ②①③
C . ③①②
D . ①②③
-
4.
(2024八上·大竹期末)
在学校的体育训练中,小杰投实心球的7次成绩就如统计图所示,则这7次成绩的中位数和众数分别是( )
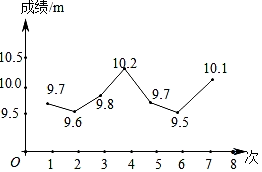
A . 9.7m,9.8m
B . 9.7m,9.7m
C . 9.8m,9.9m
D . 9.8m,9.8m
-
5.
(2020·绍兴模拟)
已知三角形纸片ABC,其中∠B=45°,将这个角剪去后得到四边形ADEC,则这个四边形的两个内角∠ADE与∠CED的和等于( )
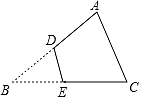
A . 235°
B . 225°
C . 215°
D . 135°
-
6.
(2020·绍兴模拟)
已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为( )
A . (1,﹣5)
B . (1,5)
C . (﹣1,5)
D . (﹣1,﹣5)
-
7.
(2020·绍兴模拟)
抛物线y=﹣x
2+bx+c与x轴的两个交点坐标如图所示,下列说法中错误的是( )
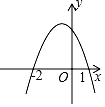
A . 一元二次方程﹣x2+bx+c=0的解是x1=﹣2,x2=1
B . 抛物线的对称轴是  C . 当x>1时,y随x的增大而增大
D . 抛物线的顶点坐标是
C . 当x>1时,y随x的增大而增大
D . 抛物线的顶点坐标是 
-
-
9.
(2020·绍兴模拟)
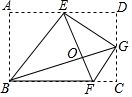
将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则

的值为( )
-
10.
(2023八下·洛阳期中)
如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以8m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示,结合题目信息,下列说法错误的是( )
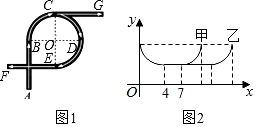
A . 立交桥总长为168 m
B . 从F口出比从G口出多行驶48m
C . 甲车在立交桥上共行驶11 s
D . 甲车从F口出,乙车从G口出
二、填空题(本大题有6小题,每小题5分,共30分)
-
-
-
13.
(2020·绍兴模拟)
中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为
.
-
-
15.
(2020·射阳模拟)
如图,点A在双曲线y=

(k<0)上,连接OA,分别以点O和点A为圆心,大于

OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为
.
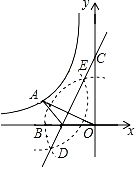
-
16.
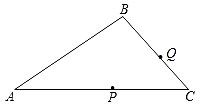
(2020八上·上虞月考)
在如图所示的三角形中,∠A=30°,点P和点Q分别是边AC和BC上的两个动点,分别连接BP和PQ,把△ABC分割成三个三角形△ABP,△BPQ,△PQC,若分割成的这三个三角形都是等腰三角形,则∠C有可能的值有
个.
三、解答题(本大题共8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题8分,第24小题14分,共80分.)
-
-
(1)
计算:(﹣

)
﹣2﹣|4﹣2
 |﹣tan60°;
|﹣tan60°;
-
(2)
若x=2是方程x2﹣4mx+m2=0的一个根,求m的值.
-
18.
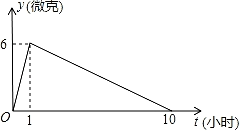
(2021·鄂尔多斯模拟)
在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似地满足图中折线.
-
(1)
求注射药物后每毫升血液中含药量y与时间t之间的函数关系式,并写出自变量的取值范围;
-
(2)
据临床观察:每毫升血液中含药量不少于4微克时,对控制病情是有效的.如果病人按规定的剂量注射该药物后,求控制病情的有效时间.
-
19.
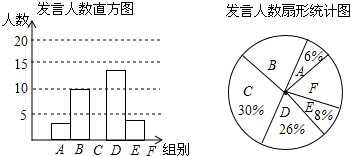
(2020·绍兴模拟)
某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
| |
发言次数n
|
|
A
|
0≤n<3
|
|
B
|
3≤n<6
|
|
C
|
6≤n<9
|
|
D
|
9≤n<12
|
|
E
|
12≤n<15
|
|
F
|
15≤n<18
|
-
-
(2)
该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
-
(3)
已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
-
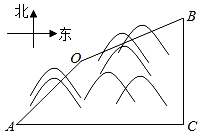
20.
(2020·绍兴模拟)
随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式,如图A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道由A地到O地,再由O地到B地可大大缩短路程、∠OAC=45°,∠OBC=60°,∠ACB=90°,AC=540公里,BC=400公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:

≈1.7,

≈1.4,

≈2.4)
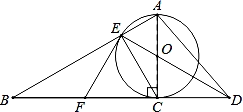
-
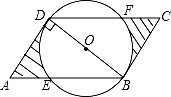
21.
(2020·绍兴模拟)
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
-
-
(2)
若⊙O的半径为3,∠EAC=60°,求AD的长.
-
22.
(2020·绍兴模拟)
熊组长准备为我们年级投资1万元围一个矩形的运动场地(如图),其中一边靠墙,另外三边选用不同材料建造且三边的总长为50m,墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用150元/m,设平行于墙的边长为x/m.

-
(1)
若运动场地面积为300m2 , 求x的值;
-
-
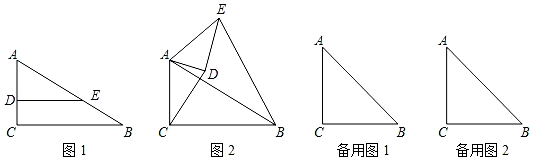
23.
(2020·绍兴模拟)
如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
-
(1)
当sinB=

时,
①求证:BE=2CD;
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
-
(2)
当sinB=

时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2

,求线段CD的长.
-
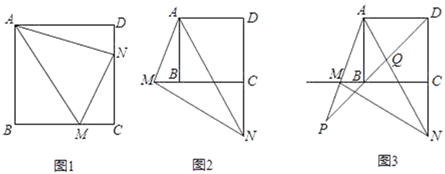
24.
(2020·绍兴模拟)
如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
-
(1)
如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
-
(2)
如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
-
(3)
如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.