
 B .
B .  C .
C .  D .
D . 
| 成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
| 人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法正确的是( )
①在直线 上任取一点B,连接
②以 为圆心,
长为半径作弧,交直线
于点
;
③分别以 为圆心,
长为半径作弧,两弧相交于点
;
④作直线 ,直线
即为所求如图(2),小红的做题依据是( )

①等边三角形、菱形、正方形、圆既是轴对称图形又是中心对称图形.
②九边形的内角和等于 ;
③ 的整数部分是x,小数部分是y,则
④一元二次方程 有两个不相等的实数根.
⑤对于命题“对顶角相等”,它的逆命题是假命题.


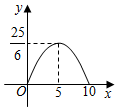 B .
B . 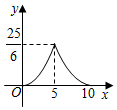 C .
C . 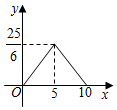 D .
D . 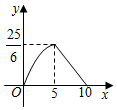




(考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34, )
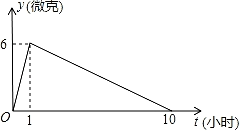
② ;
| 规格 | 线下 | 线上 | ||
| 单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
| A | 240 | 0 | 210 | 20 |
| B | 300 | 0 | 250 | 30 |


图1中,线段PM与PN的数量关系是,位置关系是;
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.