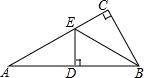
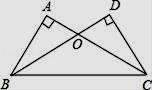
 B .
B .  D .
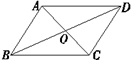
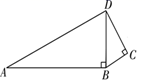
D . 
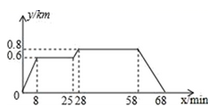
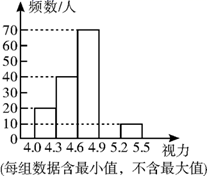
|
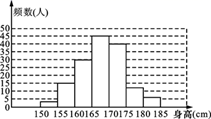
视力 |
频数/人 |
频率 |
|
4.0≤x<4.3 |
20 |
0.1 |
|
4.3≤x<4.6 |
40 |
0.2 |
|
4.6≤x<4.9 |
70 |
0.35 |
|
4.9≤x<5.2 |
a |
0.3 |
|
5.2≤x<5.5 |
10 |
b |

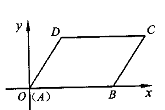
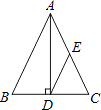
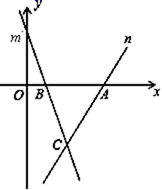
②作出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标;

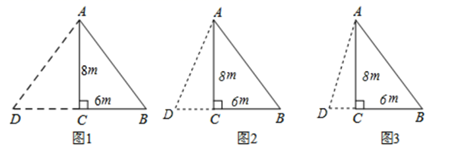
C(-1,0),点A(0,4),试求直线AB的函数表达式;