浙江省黄岩市2020年数学中考一模试卷

更新时间：2020-07-23 浏览次数：280 类型：中考模拟

一、选择题（本题有10小题，每小题4分，共40分.）

1. (2020七上·宝安期末) 2020的相反数是（）

A . 2020 B . -2020 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·浙江模拟) 为抗击新冠肺炎疫情，今年2月29日我国口罩日产能已达到116 000 000只.将116 000 000用科学记数法可表示为（）

A . 116×10⁸ B . 116×10⁶ C . 1.16×10⁸ D . 1.16×10⁶

答案解析收藏纠错 + 选题
3. (2020·浙江模拟) 如图，已知直线a//b，直线c与直线a，b分别交于点A，B.若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 126° B . 134° C . 136° D . 144°

答案解析收藏纠错 + 选题
4. (2020·浙江模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九下·安岳开学考) 用配方法解一元二次方程x²﹣4x+1=0时，下列变形正确的是（）

A . (x﹣2)²=1 B . (x﹣2)²=5 C . (x+2)²=3 D . (x﹣2)²=3

答案解析收藏纠错 + 选题
6. (2020·浙江模拟) 如图，△ABC内接于⊙O，∠A＝ $\text{[math]}$ .若BC＝ $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . π B . $\text{[math]}$ C . 2π D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·重庆开学考) 某生态示范园计划种植一批果树，原计划总产量36吨，改良果树品种后平均亩产量是原计划的1.5倍，种植亩数减少了20亩，总产量比原计划增加了9吨.设原计划平均亩产量为x吨，则根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·浙江模拟) 如图，矩形纸片ABCD中，AB=6，BC=8，E是边CD上一点，连接AE.折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上.若DE=4，则AF的长为（）

A . $\text{[math]}$ B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题

9. (2020·浙江模拟) 某辆汽车每次加油都会把油箱加满，下表记录了该车相邻两次加油时的情况.（注：“累计里程”指汽车从出厂开始累计行驶的路程）

加油时间	加油量（升）	加油时的累计里程（千米）
2020年3月10日	15	56000
2020年3月25日	50	56500

在这段时间内，该车每100千米平均耗油量为（）

A . 7升 B . 8升 C . 10升 D . $\text{[math]}$ 升

答案解析收藏纠错 + 选题

10. (2020·浙江模拟) 直线y=kx+b与坐标轴交于A、B两点，与双曲线 $\text{[math]}$ （x>0）相交于C、D两点，若C、D恰好是线段AB的三等分点，则直线y=kx+b的存在情况是（）

A . 不存在 B . 1条 C . 2条 D . 无数条

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题5分，共30分）

11. (2023九上·青秀开学考) $\text{[math]}$ =

答案解析收藏纠错 + 选题
12. (2020·浙江模拟) 二次函数y=x²-1图象的顶点坐标是.

答案解析收藏纠错 + 选题
13. (2020·浙江模拟) 同时抛掷两枚质地均匀的硬币，落地后，两枚硬币都正面向上的概率是.

答案解析收藏纠错 + 选题
14. (2020·浙江模拟) 如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形，恰好能拼成这样一个“勾股圆方图”，则该矩形与拼成的正方形的周长之比为.

答案解析收藏纠错 + 选题
15. (2022七下·雄县期末) 数学何老师网购了一本《魔法数学》，同学们想知道书的价格，何老师让他们猜.甲说：　“至少15元.”乙说：“至多25元.”丙说：“至多20元.”何老师说：“你们三个人中只有一人说对了”.则这本书的价格x（元）所在的范围为.

答案解析收藏纠错 + 选题
16. (2020·浙江模拟) 面积为1的▱ABCD的边AB和CD被分为n等份，边AD和BC被分为m等份，按如图所示的方式连接分点，则图中形成的小平行四边形的面积S =.

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）

17. (2020·浙江模拟) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2020·浙江模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2020·浙江模拟) 如图，点A、B、C是方格纸中的格点，请用无刻度的直尺作图.
1. （1）在图1中画出一个以A、B、C、D为顶点的平行四边形；
2. （2）在图2中过点C作出AB的垂线.
答案解析收藏纠错 + 选题
20. (2020·浙江模拟) 图1是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角为70°时，箱盖ADE落在AD′E′的位置（如图2所示）.已知AD＝60厘米，DC＝40厘米，求点D' 到BC的距离.
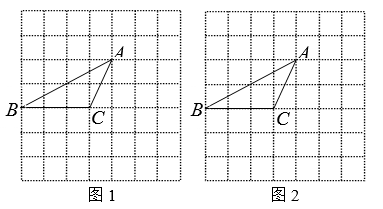
（参考数据：sin70°≈0.94，cos70°≈0.34）

答案解析收藏纠错 + 选题
21. (2020·浙江模拟) 甲、乙两校各组织300名学生参加联赛，为了解两校联赛成绩情况，在两校随机抽取部分学生的联赛成绩，两校抽取的人数相等，结果如下（数据包括左端点不包括右端点）.
1. （1）若小明是乙校的学生，他的成绩是75分，请结合数据分析小明的成绩；
2. （2）若甲校中一位同学的成绩不纳入计算后，甲校的平均成绩提高了，你认为这位同学的成绩一定不可能在哪个分数段？
3. （3）请用适当的统计量从两个不同角度分析哪所学校的联赛成绩整体较好？
答案解析收藏纠错 + 选题
22. (2020·浙江模拟) 如图1，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D.
1. （1）求证：AC平分∠DAB；
2. （2）若AD与⊙O交于点E，连接BE，交AC于点F，若点F是AC的中点，如图2，求EF∶BF的值.
答案解析收藏纠错 + 选题
23. (2020·浙江模拟) 如图1，小明用一张边长为6 dm的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为x dm，再折成如图2所示的无盖糖果盒，它的容积记为y dm³.
1. （1） y关于x的函数关系式是，自变量x的取值范围是.
2. （2）为探究y随x的变化规律，小明类比二次函数进行了如下探究：
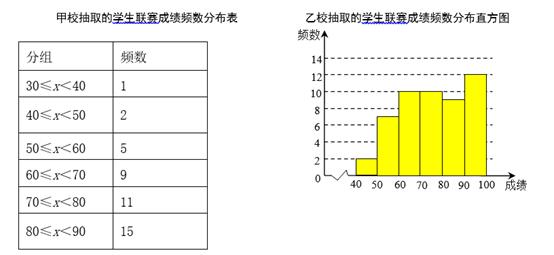
  ①列表：请你补充表格中的数据；
  
  x
  
  0
  
  0.5
  
  1
  
  1.5
  
  2
  
  2.5
  
  3
  
  y
  
  0
  
  3.125
  
  3.375
  
  0.625
  
  0
  
  ②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；
  
  ③连线：请你用光滑的曲线顺次连接各点.
3. （3）利用函数图象解决：
  ①该糖果盒的最大容积是；
  
  ②若该糖果盒的容积超过2 dm³ ，请估计糖果盒的底边长a的取值范围.（保留一位小数）
答案解析收藏纠错 + 选题
24. (2020·浙江模拟) 对于平面内的点P与射线OA，射线OA上与点P距离最近的点与端点O的距离叫做点P关于射线OA的侧边距，记作φ（P，OA）.
1. （1）在菱形OABC中，OA=2，∠OAB=45°.则φ（B，OA）=，φ（C，OA）=.
2. （2）在▱ABCD中，若φ（A，BD）=φ（C，BD），则▱ABCD是否必为正方形，请说明理由；
3. （3）如图，已知点C是射线OA上一点，CA=OA=2，以OA为半径画⊙O，点B是⊙O　上任意点，D为线段BC的中点.
  ①若φ（D，OA）= $\text{[math]}$ ，则φ（D，OB）=；
  
  ②设φ（D，OA）=x，φ（D，OB）=y，求y关于x的函数关系式并写出自变量x的取值范围.
答案解析收藏纠错 + 选题