浙江省宁波市兴宁中学2020届数学中考三模试卷

更新时间：2020-10-10 浏览次数：489 类型：中考模拟

一、选择题（每小题4分，共40分）

1. 下列各数中，绝对值最小的数是（）

A . 0 B . -4 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 中共中央总书记习近平同志在十九大报告中指出：“国内生产总值从54万亿元增长到80万亿元。”将近似数54万亿用科学记数法表示为（）

A . 54×10¹² B . 5.4×10¹³ C . 0.54×10¹⁴ D . 5×10¹³

答案解析收藏纠错 + 选题
3. 如图是某个几何体的三视图，该几何体是（）

A . 正方体 B . 圆锥 C . 圆柱 D . 球

答案解析收藏纠错 + 选题
4. 要使 $\text{[math]}$ 有意义，x的取值范围是（）

A . x≤3 B . x<3 C . x≥3 D . x>3

答案解析收藏纠错 + 选题
5. 下列图形中，是中心对称图形但不是轴对称图形的有（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. 某体育用品商店一天中卖出某种品牌的运动鞋15双，其中各种尺码的鞋的销售量如表所示：

鞋的尺码/cm

23

23.5

24

24.5

25

销售量/双

1

3

3

6

2

则这15双鞋的尺码组成的一组数据中，众数和中位数分别为（）

A . 23.5，24 B . 24.5，24 C . 24，24 D . 24.5，24.5

答案解析收藏纠错 + 选题
7. 国学经典《声律启蒙》中有这样一段话：“斜对正，假对真，韩卢对苏雁，陆橘对庄椿”，现有四张卡片依次写有一“斜”、“正”、“假”、“真”，四个字（4张卡片除了书写汉字不同外其他完全相同），现从四张卡片中随机抽取两张，则抽到的汉字恰为相反意义的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图，正方形ABCD中，点E为BC右侧一点，∠AEC=90°，作DF⊥AE于点F，若CE=AF=2则正方形的面积为（）

A . 16 B . 18 C . 20 D . 25

答案解析收藏纠错 + 选题
9. 如图，半圆O的半径长为5，点P为直径AB上的一个动点，已知CP上AB，交半圆O于点C，若D为半圆O上的一动点，且CD=4，M是CD的中点，则PM的值有（）

A . 最小值5 B . 最小值4 C . 最大值5 D . 最大值4

答案解析收藏纠错 + 选题
10. 如图1，以直角三角形的各边为斜边分別向外作等腰直角三角形，再把较小的两张等腰直角三角形纸片按图2的方式放置在最大等腰直角三角形内。若知道图中阴影部分的面积则一定能求出（）

A . 直角三角形的面积 B . 最大等腰直角三角形的面积 C . 较小两个等腰直角三角形重叠的面积 D . 最大等腰直角三角形和直角三角形的面积之和

答案解析收藏纠错 + 选题

二、填空题（每小題5分，共30分）

11. 因式分解：x²-9=。

答案解析收藏纠错 + 选题
12. 不等式组 $\text{[math]}$ 的解集为。

答案解析收藏纠错 + 选题
13. 圆锥的侧面积为16πcm²，底面圆的半径为2cm，则这个圆锥的母线长为cm。

答案解析收藏纠错 + 选题
14. 如图所示，一副篮架由配重、支架、篮板与篮筐组成，在立柱的C点观察篮板上沿D点的仰角为45°，在支架底端的A点观察篮板上沿D点的仰角为54°，点C与篮板下沿点E在同一水平线，若AB=1.91米，篮板高度DE为1.05米，那么篮板下沿E点与地面的距离为。（结果精确到0.1m，参考数据：sin54°≈0.80，cos54°≈0.60，tan54°≈1.33）

答案解析收藏纠错 + 选题
15. 如图，Rt△ACB中，∠ACB=90°，AC=2BC=4，点P为AB边中点，点D为AC边上不与端点重合的一动点，将△ADP沿着直线PD折叠得△PDE，若DE⊥AB，则AD的长度为。

答案解析收藏纠错 + 选题
16. 如图，点A、C、B是双曲线y= $\text{[math]}$ （k>0，x>0）上从右至左得三点，连结OA，OB，OC，AC，BC，△OBC和△ACO的面积相等，若A、B两点横坐标的比为4：1，则A、C两点的纵坐标的比值为。

答案解析收藏纠错 + 选题

三、解答题（本题8小题，共40分）

17.
1. （1） | $\text{[math]}$ -2|-（ $\text{[math]}$ ）^-2+ $\text{[math]}$ ×cos60°
2. （2）先化简，再求值： $\text{[math]}$ ，请从-2，-1，0，1中选择一个合适的值代入求值。
答案解析收藏纠错 + 选题
18. 如图，在由小正方形组成的4×3的网格中，△ABC的顶点都在小正方形的顶点上，用无刻度的直尺，在所给的网格中，按要求作图并保留作图痕迹。
①在图1中作△ABC的轴对称图形△A'B'C'；

②在图2中作△ABC的重心；

③在图3中作△ABC的的高线AH。

答案解析收藏纠错 + 选题
19. 某中学疫情期间为了切实抓好“停课不停学“活动，借助某软件平台随机抽取了该校部分学生的在线学习时间，并将结果给制成如下两幅不完整的统计的图。

请你根据以上信息回答下列问题：
1. （1）本次调查的人数为人，学习时间为7小时的所对的圆心角为；
2. （2）补全频数分布直方图；
3. （3）若全校共有学生1800人，估计有多少学生在线学习时间不低于8个小时。
答案解析收藏纠错 + 选题
20. 如图，已知二次函数y=-x²+bx+c的图像经过点A（4，-5），点B（0，3）。
1. （1）求b，c的值和图像的顶点坐标；
2. （2）点Q（m，n）在该二次函数图象上；
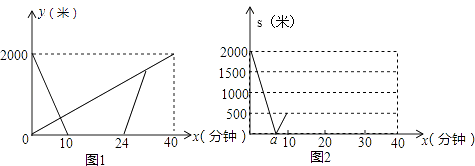
  ①当m=-2时，求n的值；
  
  ②若点Q到y轴的距离小于2，请根据图像直接写出n的取值范围；
3. （3）将（1）中图像向右平移k（k>0）个单位，使得当x>2时，y随x的增大而减小，请根据图像直接写出k的取值范围。
答案解析收藏纠错 + 选题
21. 如图，菱形ABCD的对角线AC，BD交于点O，E，F分别是AO，BO的中点，直线EF交AD，BC于点G，H。
1. （1）求证：①四边形ABHG是平行四边形；
  ②GE=HF；
2. （2）若四边形ABHG的周长为10，∠ABC=60°，求菱形ABCD的面积。
答案解析收藏纠错 + 选题
22. (2013·淮安) 甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路L步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y₁米，小亮与甲地的距离为y₂米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y₁、y₂与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．
1. （1）求小亮从乙地到甲地过程中y₂（米）与x（分钟）之间的函数关系式；
2. （2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
3. （3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．
答案解析收藏纠错 + 选题
23. 如图1，若O是AB的中点，也是CD的中点，那么点称为AB与CD的结点。
1. （1）如图2，已知四边形ABCD的对角线交于点O，且O是AC，BD的结点，请直接写出满足要求的四边形ABCD的名称（写出两个即可）
2. （2）如图3，在Rt△ABC中，∠C=90°，O是AB的中点，E是BC上一点，G是AC上一点，连结EG，过点G作EG的垂线，交EO的延长线于点∠EGC=∠GDA。求证：O是AB，DE的结点。
3. （3）在（2）的条件下，当BC=8，AC=6 $\text{[math]}$ ，且EG=DO时，求DG的长。
答案解析收藏纠错 + 选题
24. 已知AB是⊙O的直径，弦CD⊥AB于M，连结AC。
1. （1）如图1，过CD延长线上一点E作EG切⊙O于G，连接AG交CD于K；
  ①求证：KE=GE；
  
  ②如图1，若CA∥GE，tan∠AKC=3，求sin∠ACM的值；
  
  ③如图2，在②的条件下，连接CG交AB于T，若AK= $\text{[math]}$ ，求CT的长。
2. （2）如图3，连结BC、BD，BD交直径CP于N，若tan∠ABC=x，y= $\text{[math]}$ ，试用含x的式子表示y。
答案解析收藏纠错 + 选题