![]()





|
选项 |
A |
B |
C |
D |
E |
|
后续措施 |
扩大宣传力度 |
分类隔离病人 |
封闭小区 |
聘请专业物资 |
采取其他措施 |
|
选择人次 |
25 |
85 |
15 |
35 |

已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
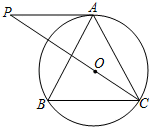

②请求出a的值;
①直接写出b的值为 ▲ ;
②求点P的坐标.
