四川省成都市新都区2020年中考数学三模试卷

更新时间：2020-08-07 浏览次数：238 类型：中考模拟

一、单选题

1. (2020·新都模拟) 钓鱼岛是中国的固有领土，其渔业资源十分丰富，年捕鱼量达16万吨，数据16万用科学记数法表示为（）

A . 1.6×10⁴ B . 1.6×10⁵ C . 16×10⁴ D . 16×10⁵

答案解析收藏纠错 + 选题
2. (2024九下·福田开学考)
如图所示的几何体的左视图为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·新都模拟) 平面直角坐标中，已知点P（a ， 3）在第二象限，则点P关于直线m（直线m上各点的横坐标都是2）对称的点的坐标是（）

A . （﹣a ， 3） B . （a ， ﹣3） C . （﹣a+2，3） D . （﹣a+4，3）

答案解析收藏纠错 + 选题
4. (2020·新都模拟) 下列计算正确的是（）

A . 2x²•3x³＝6x⁶ B . x³÷x³＝0 C . （2xy）³＝6x³y³ D . （x³）^m÷x^2m＝x^m

答案解析收藏纠错 + 选题
5. (2020·新都模拟) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ，下列条件中不能判定 $\text{[math]}$ ≌ $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·新都模拟) 如图，是某市一周内最高气温的折线统计图，关于这7天的日气温的说法，错误的是（）

A . 最高气温是30℃ B . 最低气温是20℃ C . 众数是28℃ D . 平均数是26℃

答案解析收藏纠错 + 选题
7. (2020·新都模拟) 下列结论正确的是（）

A . $\text{[math]}$ 是分式方程 B . 方程 $\text{[math]}$ ＝1无解 C . 方程 $\text{[math]}$ 的根为x＝0 D . 解分式方程时，一定会出现增根

答案解析收藏纠错 + 选题
8. (2020·新都模拟) 如图，在平行四边形ABCD中，AB＝4，AD＝5，∠B＝60°，以点B为圆心，BA为半径作圆，交BC边于点E，连接ED，则图中阴影部分的面积为（　　）

A . 9 $\text{[math]}$ ﹣ $\text{[math]}$ B . 9﹣ $\text{[math]}$ C . 9 $\text{[math]}$ D . 9﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·新都模拟) 关于二次函数 $\text{[math]}$ ，以下结论：①抛物线交x轴有两个不同的交点；②不论k取何值，抛物线总是经过一个定点；③设抛物线交x轴于A、B两点，若 $\text{[math]}$ ，则 $\text{[math]}$ ；④抛物线的顶点在 $\text{[math]}$ 图象上；⑤抛物线交y轴于C点，若 $\text{[math]}$ 是等腰三角形，则 $\text{[math]}$ ，0，1．其中正确的序号是（）

A . ①②⑤ B . ②③④ C . ①④⑤ D . ②④

答案解析收藏纠错 + 选题
10. (2020·新都模拟) 如图，在圆内接四边形ABCD中，∠C＝110°，则∠BOD的度数为（）

A . 140° B . 70° C . 80° D . 60°

答案解析收藏纠错 + 选题

二、填空题

11. (2020七上·门头沟期末)
实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是．

答案解析收藏纠错 + 选题
12. (2020八上·海曙月考) 一个等腰三角形的两条边分别是6厘米和8厘米，那么它的周长是厘米．

答案解析收藏纠错 + 选题
13. (2020·新都模拟) 把只有颜色不同的2个红球和1个白球装入一个不透明的口袋里搅匀，从中随机地一次摸出2个球，得1个红球1个白球的概率为．

答案解析收藏纠错 + 选题
14. (2020·新都模拟) 已知线段a、b、c ，如果a：b：c＝1：2：3，那么“ $\text{[math]}$ ”的值是．

答案解析收藏纠错 + 选题
15. (2020·新都模拟) 已知关于x、y的方程组 $\text{[math]}$ 中，x、y满足关系式2x﹣y＝5，则代数式a﹣a²的值为．

答案解析收藏纠错 + 选题
16. (2020·新都模拟) 四个全等的直角三角形按图示方式围成正方行ABCD，过各较长直角边的中点作垂线，围成面积为4的小正方形EFGH，已知AM为Rt△ABM的较长直角边，AM＝ $\text{[math]}$ EF，则正方形ABCD的面积为.

答案解析收藏纠错 + 选题
17. (2020·新都模拟) 阅读下列材料，然后回答问题：
已知a＞0，S₁＝ $\text{[math]}$ ，S₂＝﹣S₁﹣1，S₃＝ $\text{[math]}$ ，S₄＝﹣S₃﹣1，S₅＝ $\text{[math]}$ ，…．当n为大于1的奇数时，S_n＝ $\text{[math]}$ ；当n为大于1的偶数时，S_n＝﹣S_n_﹣₁﹣1．直接写出S₂₀₂₀＝（用含a的代数式表示）；计算：S₁+S₂+S₃+…+S₂₀₂₂＝．

答案解析收藏纠错 + 选题
18. (2020·新都模拟) 如图平面直角坐标系中放置Rt△PEF ， ∠E＝90°，EP＝EF ， △PEF绕点P（﹣1，﹣3）转动，PE、PF所在直线分别交y轴，x轴正半轴于点B（0，b），A（a ， 0），作矩形AOBC ，双曲线y＝ $\text{[math]}$ （k＞0）经过C点，当a ， b均为正整数时，k＝．

答案解析收藏纠错 + 选题

三、解答题

19. (2020·新都模拟)
1. （1）计算：﹣2²+ $\text{[math]}$ ﹣2cos30°+|1﹣ $\text{[math]}$ |；
2. （2）化简：（ $\text{[math]}$ ﹣1）÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2020·新都模拟) 已知关于x的一元二次方程kx²﹣4x+2＝0有两个不相等的实数根，求k的取值范围．

答案解析收藏纠错 + 选题

21. (2020·新都模拟) 某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试，并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图（注：在频数分布直方图中，每组含左端点，但不含右端点）：

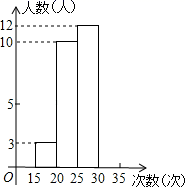
仰卧起坐次数的范围（次）	15～20	20～25	25～30	30～35
频数	3	10	12
频率	$\text{[math]}$	$\text{[math]}$		$\text{[math]}$

（1） 30～35的频数是、25～30的频率是．并把统计图补充完整；
（2）被抽查的所有女同学仰卧起坐次数的中位数是多少？

答案解析收藏纠错 + 选题

22. (2020·新都模拟) 京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点A、B和点C、D ，先用卷尺量出AB＝180m ， CD＝60m ，再用测角仪测得∠CAB＝30°，∠DBA＝60°，求该段运河的河宽（即CH的长）．

答案解析收藏纠错 + 选题
23. (2020·新都模拟) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 两点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点D， $\text{[math]}$ ， $\text{[math]}$ ，B点的坐标为 $\text{[math]}$ ．
1. （1）求一次函数和反比例函数的表达式；
2. （2）求 $\text{[math]}$ 的面积；
3. （3） P是y轴上一点，且 $\text{[math]}$ 是等腰三角形，请直接写出所有符合条件的P点坐标．
答案解析收藏纠错 + 选题
24. (2020·新都模拟) 如图，AB 是⊙O的直径，∠DAB的角平分线AC交⊙O于点C ，过点C作CD⊥AD于D ， AB的延长线与DC的延长线相交于点P ， ∠ACB的角平分线CE交AB于点F、交⊙O于E ．
1. （1）求证：PC与⊙O相切；
2. （2）求证：PC＝PF；
3. （3）若AC＝8，tan∠ABC＝ $\text{[math]}$ ，求线段BE的长．
答案解析收藏纠错 + 选题
25. (2020·新都模拟) 如图，△ABC 为等腰直角三角形，∠ACB＝90°，点 M 为 AB 边的中点，点 N 为射线 AC 上一点，连接 BN，过点 C 作 CD⊥BN 于点 D，连接 MD，作∠BNE＝∠BNA，边 EN 交射线 MD 于点 E，若 AB＝20 $\text{[math]}$ ，MD＝14 $\text{[math]}$ ，求则 NE 的长

答案解析收藏纠错 + 选题
26. (2020八下·平罗期末) 一家蔬菜公司计划到某绿色蔬菜基地收购A，B两种蔬菜共140吨，预计两种蔬菜销售后获利的情况如表所示：

销售品种

A种蔬菜

B种蔬菜

每吨获利（元）

1200

1000

其中A种蔬菜的5%、B种蔬菜的3%须运往C市场销售，但C市场的销售总量不超过5.8吨．设销售利润为W元（不计损耗），购进A种蔬菜x吨．
1. （1）求W与x之间的函数关系式；
2. （2）将这140吨蔬菜全部销售完，最多可获得多少利润？
答案解析收藏纠错 + 选题
27. (2020·新都模拟) 如图，菱形ABCD的边长为20cm ， ∠ABC＝120°．动点P、Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q先以2 $\text{[math]}$ cm/s的速度沿A→O的路线向点O运动，然后再以2cm/s的速度沿O→D的路线向点D运动，当P、Q到达终点时，整个运动随之结束，设运动时间为t秒．
1. （1）在点P在AB上运动时，判断PQ与对角线AC的位置关系，并说明理由；
2. （2）若点Q关于菱形ABCD的对角线交点O的对称点为M ，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N ．
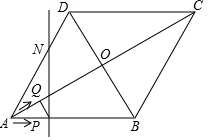
  ①直接写出当△PQM是直角三角形时t的取值范围；
  
  ②是否存在这样的t ，使△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
28. (2020·新都模拟) 已知：在平面直角坐标系中，抛物线y＝ax²﹣2ax+4（a＜0）交x轴于点A、B，与y轴交于点C，AB＝6．
1. （1）如图1，求抛物线的解析式；
2. （2）如图2，点R为第一象限的抛物线上一点，分别连接RB、RC，设△RBC的面积为s，点R的横坐标为t，求s与t的函数关系式；
3. （3）在（2）的条件下，如图3，点D在x轴的负半轴上，点F在y轴的正半轴上，点E为OB上一点，点P为第一象限内一点，连接PD、EF，PD交OC于点G，DG＝EF，PD⊥EF，连接PE，∠PEF＝2∠PDE，连接PB、PC，过点R作RT⊥OB于点T，交PC于点S，若点P在BT的垂直平分线上，OB﹣TS＝ $\text{[math]}$ ，求点R的坐标．
答案解析收藏纠错 + 选题