| 册数/册 | 1 | 2 | 3 | 4 | 5 |
| 人数/人 | 2 | 5 | 7 | 4 | 2 |
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
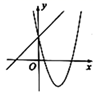 B .
B .  C .
C . 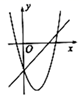 D .
D . 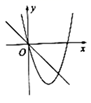
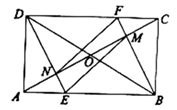
① ;②
;③
;④当
时,四边形
是菱形.其中,正确结论的个数是( )


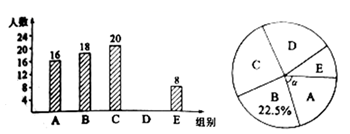
根据统计图中的信息解答下列问题: