 B .
B .  C .
C .  D .
D . 
| 分数/分 | 85 | 88 | 91 | 94 |
| 人数/人 | 2 | 3 | 4 | 1 |
那么,这10名选手得分的中位数和众数分别是( )
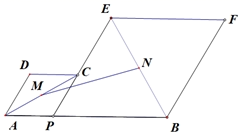

请根据以上图表提供的信息,解答下列问题:
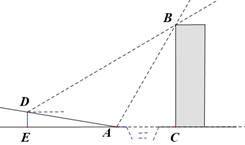



①当点 在点
右侧时,连接AF,当
时,求
的长.
②当点 在运动时,若
、
、
中有两条线段相等,求此时点
的坐标.




