湖北省襄阳市保康县2020年数学中考适应性试卷

更新时间：2024-11-06 浏览次数：245 类型：中考模拟

一、选择题

1. (2024·玉山模拟) －3的倒数是（）

A . 3 B . －3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·保康模拟) 2019年，保康县全年投入资金3593万元，实施学校建设项目16个，新建、改扩建校舍20398平方米.其中20398m²用科学记数法可表示为（）

A . 20.4×10³m² B . 2.03×10⁴m² C . 2.04×10⁴m² D . 3.60×10³万元

答案解析收藏纠错 + 选题
3. (2024七下·玉州期中) 如图，直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α的余角等于（）

A . 19° B . 38° C . 42° D . 52°

答案解析收藏纠错 + 选题
4. (2020·保康模拟) 下列计算正确的是（）

A . 3x²y＋5xy＝8x³y² B . （x＋y）²＝x＋y C . （－2x）²÷x＝4x D . a⁶÷a³＝a²

答案解析收藏纠错 + 选题
5. (2021·巴州模拟) “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（）

A . 1.25尺 B . 56.5尺 C . 6.25尺 D . 57.5尺

答案解析收藏纠错 + 选题
6. (2021·巴州模拟) 如图，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为（）

A . 60πcm² B . 65πcm² C . 120πcm² D . 130πcm²

答案解析收藏纠错 + 选题
7. (2020八下·潮安期末) 某中学对该校九年级45名女学生进行了一次立定跳远测试，成绩如表：
跳远成绩
160
170
180
190
200
210
人数
3
9
6
9
15
3
这些立定跳远成绩的中位数和众数分别是（）

A . 9，9 B . 15，9 C . 190，200 D . 185，200

答案解析收藏纠错 + 选题
8. (2021九上·瑶海月考) 二次函数y＝ax²＋bx＋c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（）

A . a＜0 B . b＜0 C . c＜0 D . a＜b

答案解析收藏纠错 + 选题
9. (2020·保康模拟) 如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE=1.5，则四边形EFCD的周长为（）

A . 14 B . 13 C . 12 D . 10

答案解析收藏纠错 + 选题
10. (2023·长清模拟) 如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为(0，3 $\text{[math]}$ )，∠ABO＝30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为（）

A . ( $\text{[math]}$ ， $\text{[math]}$ ) B . (2， $\text{[math]}$ ) C . ( $\text{[math]}$ ， $\text{[math]}$ ) D . ( $\text{[math]}$ ，3﹣ $\text{[math]}$ )

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·深圳月考) 分解因式： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
12. (2020·保康模拟) 已知一元二次方程x²－3x－2＝0的两个实数根为x₁ ， x₂ ，则(x₁－1)(x₂－1)的值是.

答案解析收藏纠错 + 选题
13. (2022·中卫期中) 经过某十字路口的汽车，可直行，也可向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过该十字路口时都直行的概率是．

答案解析收藏纠错 + 选题
14. (2020·保康模拟) 如图，在 $\text{[math]}$ 中，以点A为圆心，AB的长为半径的圆恰好与CD相切于点C，交AD于点E，延长BA与 $\text{[math]}$ 相交于点F.若 $\text{[math]}$ 的长为 $\text{[math]}$ ，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2020·保康模拟) 如图，在△ABC中，AB＝AC＝10，点D是边BC上一动点（不与B、C重合），∠ADE＝∠B＝α，DE交AC于点E，且cos∠α＝ $\text{[math]}$ ，下列结论：①△ADE∽△ACD；②当BD＝6时，△ABD与△DCE全等；③△DCE为直角三角形时，BD为8或 $\text{[math]}$ ；④0＜CE≤6.4.其中正确的结论是.（把你认为正确结论的序号都填上）

答案解析收藏纠错 + 选题
16. (2020·保康模拟) 如图，在矩形ABCD中，AB＝4，∠DCA＝30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE＝30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是.

答案解析收藏纠错 + 选题

三、解答题

17. (2020·保康模拟) 化简：（ $\text{[math]}$ ）÷ $\text{[math]}$ .

答案解析收藏纠错 + 选题

18. (2024九上·梅河口期末) 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中选出一类最喜爱的电视节目，以下是根据调查结果绘制的统计图表的一部分.

类别	A	B	C	D	E
类型	新闻	体育	动画	娱乐	戏曲
人数	11	20	40	m	4

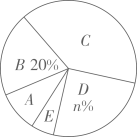
请你根据以上信息，回答下列问题：

（1）统计表中m的值为，统计图中n的值为，A类对应扇形的圆心角为度；
（2）该校共有1500名学生，根据调查结果，估计该校最喜爱体育节目的学生人数；
（3）样本数据中最喜爱戏曲节目的有4人，其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演，请用树状图或列表求所选2名同学中有男生的概率.

答案解析收藏纠错 + 选题

19. (2020·保康模拟) 为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图.小明同学为测量宣传牌的高度 $\text{[math]}$ ，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，同时测得教学楼窗户D处的仰角为 $\text{[math]}$ (A、B、D、E在同一直线上).然后，小明沿坡度 $\text{[math]}$ 的斜坡从C走到F处，此时 $\text{[math]}$ 正好与地面 $\text{[math]}$ 平行.
1. （1）求点F到直线 $\text{[math]}$ 的距离(结果保留根号)；
2. （2）若小明在F处又测得宣传牌顶部A的仰角为 $\text{[math]}$ ，求宣传牌的高度 $\text{[math]}$ (结果精确到0.1米， $\text{[math]}$ ， $\text{[math]}$ ).
答案解析收藏纠错 + 选题
20. (2020·保康模拟) 如图，一次函数y=kx＋b与反比例函数y= $\text{[math]}$ 的图象相交于A(2，4)、B(－4，n)两点.
1. （1）分别求出一次函数与反比例函数的表达式；
2. （2）根据所给条件，请直接写出不等式kx＋b＞ $\text{[math]}$ 的解集；
3. （3）过点B作BC⊥x轴，垂足为点C，连接AC，求S_△_ABC.
答案解析收藏纠错 + 选题
21. (2021八下·沂源期中) 春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如下收费标准：

某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元，请问该单位这次共有多少员工去天水湾风景区旅游？

答案解析收藏纠错 + 选题
22. (2020·保康模拟) 如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点，过点D作DF⊥AC，垂足为点F.
1. （1）求证：DF是⊙O的切线；
2. （2）若AE＝4，cosA＝ $\text{[math]}$ ，求DF的长.
答案解析收藏纠错 + 选题
23. (2020九上·枣阳期中) 某公司开发出一款新的节能产品，该产品的成本价为6元/件，该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售，售价为8元/件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象(如图)，图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系，已知线段DE表示的函数关系中，时间每增加1天，日销售量减少5件.
1. （1）第24天的日销售量是件，日销售利润是元；
2. （2）求y与x之间的函数关系式，并写出x的取值范围；
3. （3）日销售利润不低于640元的天数共有多少天？试销售期间，日销售最大利润是多少元？
答案解析收藏纠错 + 选题
24. (2020·保康模拟) 如图①所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N.
1. （1）（问题引入）若点O是AC的中点， $\text{[math]}$ ，求 $\text{[math]}$ 的值；温馨提示：过点A作MN的平行线交BN的延长线于点G.
2. （2）（探索研究）若点O是AC上任意一点(不与A，C重合)，求证： $\text{[math]}$ ；
3. （3）（拓展应用）如图②所示，点P是△ABC内任意一点，射线AP，BP，CP分别交BC，AC，AB于点D，E，F.若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2020·保康模拟) 如图1，在平面直角坐标系中，已知抛物线y＝ax²+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C.
1. （1）求抛物线的函数表达式；
2. （2）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标；
3. （3）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标.
答案解析收藏纠错 + 选题