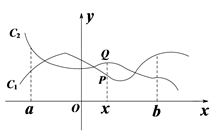B .
B .  C .
C .  D .
D . 
 B .
B . 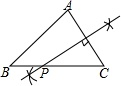 C .
C . 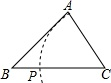 D .
D . 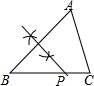
|
x |
… |
-5 |
-4 |
-3 |
-2 |
-1 |
… |
|
y |
… |
3 |
-2 |
-5 |
-6 |
-5 |
… |
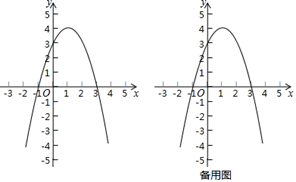
则关于x的一元二次方程ax2+bx+c=-2的根是.
|
|
中位数 |
众数 |
|
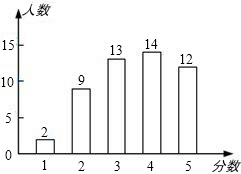
随机抽取的50人的社会实践活动成绩 |
|
|
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.

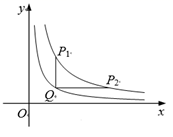
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.