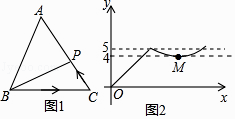
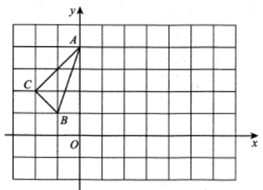
如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是.
 C .
C .  D .
D . 
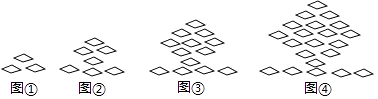
下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
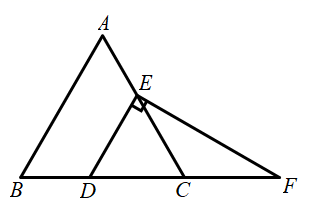

求证: .

调查结果统计表
|
组别 |
分组(单位:元) |
人数 |
|
| | |
| | | |
| | | |
| | | |
| | | |
调查结果扇形统计图
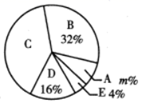
请根据以上图表,解答下列问题:
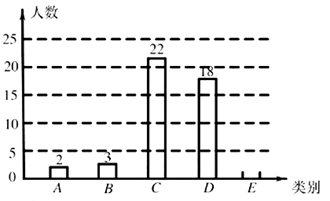
根据以上信息,解答下列问题:
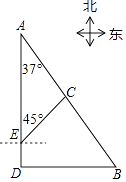
如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)