山东省济宁市梁山县2021年中考数学一模试卷

更新时间：2024-07-13 浏览次数：185 类型：中考模拟

一、单选题

1. (2022九下·吉林开学考) 已知a是 $\text{[math]}$ ，则a的倒数为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . -2

答案解析收藏纠错 + 选题
2. (2021·梁山模拟) 若 $\text{[math]}$ 与 $\text{[math]}$ 为同类项，则m-n（）

A . -4 B . -3 C . -2 D . -1

答案解析收藏纠错 + 选题
3. (2023八下·休宁期中) 围棋起源于中国，古代称之为“弈”，至今已有 $\text{[math]}$ 多年的历史． $\text{[math]}$ 年 $\text{[math]}$ 月，世界围棋冠军柯洁与人工智能机器人 $\text{[math]}$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024九下·自贡期中) 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（）

A . 22×10^﹣10 B . 2.2×10^﹣10 C . 2.2×10^﹣9 D . 2.2×10^﹣8

答案解析收藏纠错 + 选题
5. (2021·梁山模拟) 下列几何体中，其左视图和俯视图相同的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2024八下·剑阁月考) 函数 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 0 B . 2 C . 4 D . 8

答案解析收藏纠错 + 选题
7. (2021·梁山模拟) 在一个不透明的口袋中，装有a个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后放回口袋中，摸到黄球的概率是0.2，则a的值是（）

A . 16 B . 20 C . 25 D . 30

答案解析收藏纠错 + 选题
8. (2023九上·子陵月考) 一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）

A . 5：4 B . 5：2 C . $\text{[math]}$ ：2 D . $\text{[math]}$ ： $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·梁山模拟)
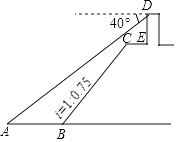
如图，小王在长江边某瞭望台D处，测得江面上的渔船A的俯角为40°，若DE=3米，CE=2米，CE平行于江面AB，迎水坡BC的坡度i=1：0.75，坡长BC=10米，则此时AB的长约为（）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）．

A . 5.1米 B . 6.3米 C . 7.1米 D . 9.2米

答案解析收藏纠错 + 选题
10. (2021·梁山模拟)
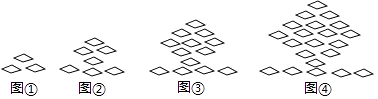
下列图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第⑨个图形中菱形的个数为（）

A . 73 B . 81 C . 91 D . 109

答案解析收藏纠错 + 选题

二、填空题

11. (2021·梁山模拟) 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改成横排，如图1、图2，图中各行从左到右列出的算筹数分别表示未知数 $\text{[math]}$ 的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 $\text{[math]}$ 类似地，图2所示的算筹图，可以表述为．

答案解析收藏纠错 + 选题
12. (2022·西安模拟) 已知矩形ABCD的四个顶点均在反比例函数y= $\text{[math]}$ 的图象上，且点A的横坐标是2，则矩形ABCD的面积为．

答案解析收藏纠错 + 选题
13. (2021·梁山模拟) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2021·梁山模拟)
如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于．

答案解析收藏纠错 + 选题
15. (2021·梁山模拟) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E是对角线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，过点E作 $\text{[math]}$ ，交 $\text{[math]}$ 于点F ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点G ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点N ，若点F是 $\text{[math]}$ 边的中点，则 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题

三、解答题

16. (2021·梁山模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2020七上·槐荫期末) 每年夏天全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某中学为确保学生安全，开展了“远离溺水，珍爱生命”的防溺水安全竞赛，学校对参加比赛的学生获奖情况进行了统计，绘制了如下两幅不完整的统计图，请结合图中相关数据解答下列问题．
1. （1）求参加此安全竞赛的学生共有多少人；
2. （2）在扇形统计图中，“三等奖”所对应的扇形的圆心角的度数为多少度？
3. （3）求获得二等奖的人数，并将条形统计图补充完整．
答案解析收藏纠错 + 选题
18. (2021·梁山模拟) 某水果店第一次用600元购进水果若干千克，第二次又用600元购进该水果，但这次每千克的进价比第一次进价的提高了25%，购进数量比第一次少了30千克．
1. （1）求第一次每千克水果的进价是多少元？
2. （2）若要求这两次购进的水果按同一价格全部销售完毕后获利不低于420元，问每千克售价至少是多少元？
答案解析收藏纠错 + 选题
19. (2021·章贡模拟) 如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．
1. （1）求证：DB=DE；
2. （2）若AB=12，BD=5，求⊙O的半径．
答案解析收藏纠错 + 选题
20. (2021·梁山模拟) 综合与实践
背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形，例如：三边长分别为9，12，15或3 $\text{[math]}$ ，4 $\text{[math]}$ ，5 $\text{[math]}$ 的三角形就是（3，4，5）型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．

实践操作如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．

第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．

第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．

第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．
1. （1）问题解决
  请在图2中证明四边形AEFD是正方形．
2. （2）请在图4中判断NF与ND′的数量关系，并加以证明；
3. （3）请在图4中证明△AEN（3，4，5）型三角形；
4. （4）探索发现
  在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．
答案解析收藏纠错 + 选题
21. (2021·梁山模拟) 阅读下列材料，并解答后面的问题．
在学习了直角三角形的边角关系后，小颖和小明两个学习小组继续探究任意锐角三角形的边角关系：在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c ．
1. （1）小明学习小组发现如下结论：
  如图1，过A作AD⊥BC于D ，则sinB= $\text{[math]}$ ，sinC= $\text{[math]}$ 即AD=csinB ， AD=bsinC ，于是=即 $\text{[math]}$ ，同理有 $\text{[math]}$ ， $\text{[math]}$
  
  则有 $\text{[math]}$
2. （2）小颖学习小组则利用圆的有关性质也得到了类似的结论：
  如图2，△ABC的外接圆半径为R ，连结CO并延长交⊙O于点D ，连结DB ，则∠D=∠A ，
  
  ∵CD为⊙O的直径，∴∠DBC=90°，
  
  在Rt△DBC中，
  
  ∵ $\text{[math]}$ ，
  
  ∴ $\text{[math]}$ ， $\text{[math]}$
  
  同理： $\text{[math]}$ ，
  
  则有 $\text{[math]}$
  
  请你将这一结论用文字语言描述出来：．
  
  小颖学习小组在证明过程中略去了“ $\text{[math]}$ ”的证明过程，请你把“ $\text{[math]}$ ”的证明过程补写出来．
3. （3）直接用前面阅读材料中得出的结论解决问题
  规划局为了方便居民，计划在三个住宅小区A、B、C之间修建一座学校，使它到三个住宅小区的距离相等，已知小区C在小区B的正东方向 $\text{[math]}$ 千米处，小区A在小区B的东北方向，且A与C之间相距 $\text{[math]}$ 千米，求学校到三个小区的距离及小区A在小区C的什么方向？
答案解析收藏纠错 + 选题
22. (2021·梁山模拟) 如图1，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与x轴相交于 $\text{[math]}$ 两点，顶点为 $\text{[math]}$ ，设点 $\text{[math]}$ 是x轴的正半轴上一点，将抛物线C绕点F旋转 $\text{[math]}$ ，得到新的抛物线 $\text{[math]}$ ．
1. （1）求抛物线C的函数表达式；
2. （2）若抛物线 $\text{[math]}$ 与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．
3. （3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线 $\text{[math]}$ 上的对应点 $\text{[math]}$ ，设M是C上的动点，N是 $\text{[math]}$ 上的动点，试探究四边形 $\text{[math]}$ 能否成为正方形？若能，求出m的值；若不能，请说明理由．
答案解析收藏纠错 + 选题