辽宁省鞍山市铁西区、立山区2020届九年级上学期数学期中考试...

更新时间：2020-10-16 浏览次数：273 类型：期中考试

一、选择题

1. (2023·化州模拟) 下列航空公司的标志中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019九上·扎兰屯期末) 关于x的方程（a﹣1）x^|a|+1﹣3x+2＝0是一元二次方程，则（）

A . a≠±1 B . a＝1 C . a＝﹣1 D . a＝±1

答案解析收藏纠错 + 选题
3. (2019九上·立山期中) 若2是一元二次方程x²+mx﹣4m＝0的一个根，则另一个根是（）

A . ﹣4 B . 4 C . ﹣6 D . 6

答案解析收藏纠错 + 选题
4. (2019九上·立山期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 5

答案解析收藏纠错 + 选题
5. (2023九上·江油月考) 如图，将△ABC绕点C顺时针旋转90°得到△EDC ．若点A ， D ， E在同一条直线上，∠ACB=20°，则∠ADC的度数是（）

A . 55° B . 60° C . 65° D . 70°

答案解析收藏纠错 + 选题
6. (2022九下·淮南月考) 如图，在△ABC中，点D、E分别在边AB，AC上，连接CD、BE交于点O，且DE∥BC，OD＝1，OC＝3，AD＝2，则AB的长为（　　）

A . 4 B . 6 C . 8 D . 9

答案解析收藏纠错 + 选题
7. (2019九上·立山期中) 用配方法解下列方程时，配方有错误的是（）

A . $\text{[math]}$ 化为 $\text{[math]}$ B . $\text{[math]}$ 化为 $\text{[math]}$ C . $\text{[math]}$ 化为 $\text{[math]}$ D . $\text{[math]}$ 化为 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·长汀期中) 已知 $\text{[math]}$ 是非零实数， $\text{[math]}$ ，在同一平面直角坐标系中，二次函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的大致图象不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2019九上·立山期中) 一元二次方程x²﹣2x﹣5＝0和x²+4x+5＝0的所有实数根的和等于.

答案解析收藏纠错 + 选题
10. (2024九上·广州期末) 已知二次函数的图象经过点 $\text{[math]}$ ，顶点为 $\text{[math]}$ 将该图象向右平移，当它再次经过点 $\text{[math]}$ 时，所得抛物线的函数表达式为.

答案解析收藏纠错 + 选题
11. (2019九上·立山期中) 如图，⊙O内有一条弦BC，A为⊙O内一点、其中OA＝3，AB＝4，∠A＝∠B＝60°，则弦BC的长为.

答案解析收藏纠错 + 选题
12. (2019九上·盂县期末) 在平面直角坐标系中，点 $\text{[math]}$ 的坐标分别是 $\text{[math]}$ ，以点 $\text{[math]}$ 为位似中心，相们比为 $\text{[math]}$ ，把 $\text{[math]}$ 缩小，得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
13. (2019九上·立山期中) 若二次函数y＝4x²﹣6x﹣3的图象与x轴交于点A（x₁ ， 0），B（x₁ ， 0）两点，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2019九上·立山期中) 股市规定：股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．若一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为x，则x满足的方程是．

答案解析收藏纠错 + 选题
15. (2019九上·立山期中) 如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B＝120°，OA＝1，将菱形OABC绕原点顺时针旋转105°至OA'B′C'的位置，则点B'的坐标为.

答案解析收藏纠错 + 选题
16. (2019九上·立山期中)
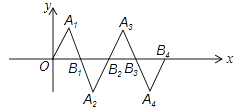
在如图所示的平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₂A₂B₁与△OA₁B₁关于点B₁成中心对称，再作△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，如此作下去，则△B_2nA_2n+1B_2n+1（n是正整数）的顶点A_2n+1的坐标是．

答案解析收藏纠错 + 选题

三、解答题

17. (2019九上·立山期中)
1. （1）解方程： $\text{[math]}$
2. （2）用配方法解方程： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2019九上·立山期中) 如图，图中的小方格都是边长为1的正方形，△ABC的A，B，C三点坐标为A（2，0）、B（2，2）、C（6，3）。
1. （1）请在图中画出一个△ $\text{[math]}$ ，使△ $\text{[math]}$ 与△ABC是以坐标原点为位似中心，相似比为2的位似图形。
2. （2）求△ $\text{[math]}$ 的面积。
答案解析收藏纠错 + 选题
19. (2021九上·察哈尔右翼前旗期末) 关于的一元二次方程x²+2x+k+1=0的实数解是x₁和x₂ ．
1. （1）求k的取值范围；
2. （2）如果x₁+x₂﹣x₁x₂＜﹣1且k为整数，求k的值．
答案解析收藏纠错 + 选题
20. (2019九上·立山期中) 如图，在甲、乙两座楼正中间有一堵院墙，小明站在甲楼某层窗口前，同时小光站在乙楼某层窗口前观察这堵墙，小明视线所及位置如图所示，小光视线恰好落在甲楼底部.已知墙的高度为5米，两栋楼的间距为100米，小明视线所及位置到墙的距离为10米.
1. （1）请根据题意画出平面图形，并标上相应字母.
2. （2）求甲、乙两人的观测点到地面高度的距离差.
答案解析收藏纠错 + 选题
21. (2023九上·张湾期中) 如图，一圆弧形桥拱的圆心为 $\text{[math]}$ ，拱桥的水面跨度 $\text{[math]}$ 米，桥拱到水面的最大高度 $\text{[math]}$ 为 $\text{[math]}$ 米.求：
1. （1）桥拱的半径；
2. （2）现水面上涨后水面跨度为 $\text{[math]}$ 米，求水面上涨的高度为米.
答案解析收藏纠错 + 选题
22. (2019九上·立山期中) 在矩形ABCD中，已知AD＞AB.在边AD上取点E，使AE＝AB，连结CE，过点E作EF⊥CE，与边AB或其延长线交于点F.
1. （1）如图1，当点F在边AB上时，线段AF与DE的大小关系为.
2. （2）如图2，当点F在边AB的延长线上时，EF与边BC交于点G.判断线段AF与DE的大小关系，并加以证明.
3. （3）如图2，若AB＝2，AD＝5，求线段BG的长.
答案解析收藏纠错 + 选题
23. (2019九上·立山期中) 随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点.抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆.已知2006年底全市汽车拥有量为10万辆.
1. （1）求2006年底至2008年底我市汽车拥有量的年平均增长率；
2. （2）为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）
答案解析收藏纠错 + 选题
24. (2019九上·立山期中) 某店铺经营某种品牌童装，购进时的单价是40元，根据市场调查，当销售单价是60元时，每天销售量是200件，销售单价每降低1元，就可多售出20件.
1. （1）求出销售量y件）与销售单价x（元）之间的函数关系式；
2. （2）求出销售该品牌童装获得的利润W（元）与销售单价x元）之间的函数关系式；
3. （3）若装厂规定该品牌童装的销售单价不低于56元且不高于60元，则此服装店销售该品牌童装获得的最大利润是多少？
答案解析收藏纠错 + 选题
25. (2024九上·乾安期末) 如图1是实验室中的一种摆动装置， $\text{[math]}$ 在地面上，支架 $\text{[math]}$ 是底边为 $\text{[math]}$ 的等腰直角三角形，摆动臂长 $\text{[math]}$ 可绕点A旋转，摆动臂 $\text{[math]}$ 可绕点D旋转， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）在旋转过程中：
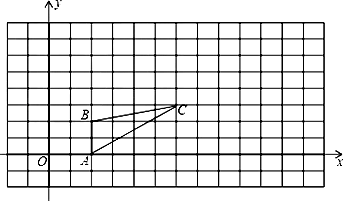
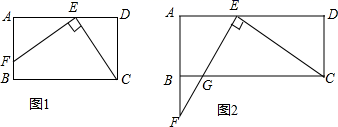
  ①当 $\text{[math]}$ 三点在同一直线上时，求 $\text{[math]}$ 的长；
  
  ②当 $\text{[math]}$ 三点在同一直角三角形的顶点时，求 $\text{[math]}$ 的长.
2. （2）若摆动臂 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，点 $\text{[math]}$ 的位置由 $\text{[math]}$ 外的点 $\text{[math]}$ 转到其内的点 $\text{[math]}$ 处，连结 $\text{[math]}$ ，如图2，此时 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
26. (2019九上·立山期中) 如图，已知抛物线与坐标轴交于A（﹣4，0）、B（2，0）、C（0，4），连接BC，AC.
1. （1）求抛物线的解析式；
2. （2）若点E是抛物线在第二象限上的一点，过点E作DE⊥AC于点D，求DE的最大值.
3. （3）若点E是抛物线上第二象限上的一动点，过点E作DE⊥AC于点D，连接CE，若△CDE与△COB相似，直接写出点E的坐标.
答案解析收藏纠错 + 选题