初中数学浙教版九年级上学期期中复习专题5 用频率估计概率

更新时间：2020-10-22 浏览次数：117 类型：复习试卷

一、单选题

1. (2020九上·宁波月考) 口袋中有白球和红球共10个，这些球除颜色外其它都相同．小明将口袋中的球搅匀后随机从中摸出一个球，记下颜色后放回口袋中，小明继续重复这一过程，共摸了100次，结果有40次是红球，请你估计口袋中红球的个数是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
2. (2020·芜湖模拟) 某校生物兴趣小组为了解种子发芽情况，重复做了大量种子发芽的实验，结果如下：

根据以上数据，估计该种子发芽的概率是（）

A . 0.90 B . 0.98 C . 0.95 D . 0.91

答案解析收藏纠错 + 选题

3. (2020七下·顺德月考) 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

则符合这一结果的实验最有可能的是（）

A . 一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是梅花 B . 抛一枚硬币，出现反面的概率 C . 袋子里有除了颜色都一样3个红球，2个白球,随机摸一个球是白球的概率 D . 抛一个质地均匀的正六面体骰子，向上的面点数大于4

答案解析收藏纠错 + 选题

4. (2024九上·石林月考) 用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，那么掷一枚质地均匀的硬币10次，下列说法正确的是（）

A . 每两次必有1次正面向上 B . 可能有5次正面向上 C . 必有5次正面向上 D . 不可能有10次正面向上

答案解析收藏纠错 + 选题
5. (2020九上·沈河期末) 如图是某小组做用频率估计概率“的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（）

A . 抛一枚硬币，出现正面朝上 B . 从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球 C . 一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D . 掷一枚均匀的正六面体骰子，出现3点朝上

答案解析收藏纠错 + 选题
6. (2020九上·中山期末) 某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼，通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右，可估计该鱼塘中草鱼的数量为（）

A . 150 B . 100 C . 50 D . 200

答案解析收藏纠错 + 选题
7. (2019九上·成都月考) 在一个不透明的布袋中装有50个红、蓝两种颜色的球，除颜色外其他都相同，小明通过多次摸球实验后发现，摸到红球的频率稳定在0.3左右，则布袋中蓝球可能有（）

A . 35个 B . 20个 C . 30个 D . 15个

答案解析收藏纠错 + 选题
8. (2019九上·长兴月考) 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表

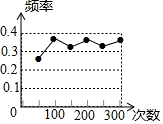
抛掷次数

100

200

300

400

500

正面朝上的频数

53

98

156

202

244

若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（）

A . 200 B . 300 C . 500 D . 800

答案解析收藏纠错 + 选题
9. (2020九上·凌海期中) 在大量重复试验中，关于随机事件发生的频率和概率，下列说法正确的是（）

A . 频率就是概率 B . 频率与试验次数无关 C . 在相同的条件下进行试验，如果试验次数相同，则各实验小组所得频率的值也会相同 D . 随着试验次数的增加，频率一般会逐步稳定在概率数值附近

答案解析收藏纠错 + 选题
10. (2020九上·商河期末) 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

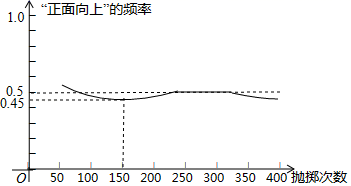
下面有三个推断：

①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；

②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；

③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．

其中合理的是（　　）

A . ① B . ② C . ①② D . ①③

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·南明月考) 在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是.

答案解析收藏纠错 + 选题
12. (2021七下·本溪期末) 技术变革带来产品质量的提升.某企业技术变革后，抽检某一产品2020件，欣喜发现产品合格的频率已达到0.9911，依此我们可以估计该产品合格的概率为.（结果要求保留两位小数）

答案解析收藏纠错 + 选题

13. (2024九下·海淀模拟) 下表记录了一名篮球运动员在罚球线上投篮的结果：

投篮次数n	48	82	124	176	230	287	328
投中次数m	33	59	83	118	159	195	223
投中频率 $\text{[math]}$	0.69	0.72	0.67	0.67	0.69	0.68	0.68

根据上表，这名篮球运动员投篮一次，投中的概率约为．（结果精确到0.01）

答案解析收藏纠错 + 选题

14. (2020·萧山模拟) 在一个布袋中装有只有颜色不同的a个小球，其中红球的个数为2，随机摸出一个球记下颜色后再放回袋中，通过大量重复实验后发现，摸到红球的频率稳定于0.2，那么可以推算出a大约是.

答案解析收藏纠错 + 选题
15. (2019九上·鼓楼期中) 不透明的盒中装着大小、外形、质地一样的红色、黑色、白色的乒乓球共20个，通过多次摸球实验后发现其中摸到红色、黑色球的概率稳定在5%和15%，则盒子中白色球的个数很可能是个．

答案解析收藏纠错 + 选题
16. (2020九上·嵩县期末) 一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小文在袋中放入3个白球(每个球除颜色外其余都与红球相同).摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.7左右，则袋中红球约有个.

答案解析收藏纠错 + 选题
17. (2019九上·平顶山期中) 为了检验某批足球的质量，随机抽取了100个足球，发现合格的有90个.如果从这批足球中随机取出一个，那么这个足球合格的概率约为.

答案解析收藏纠错 + 选题
18. (2019七下·李沧期末) 有五个面的石块，每个面上分别标记1，2，3，4，5，现随机投掷100次，每个面落在地面上的次数如下表，估计石块标记3的面落在地面上的概率是.

石块的面

1

2

3

4

5

频数

17

28

15

16

24

答案解析收藏纠错 + 选题

三、解答题

19. 为了估计鱼塘中鱼的条数，养鱼者首先从鱼塘中打捞30条鱼做上标记，然后放归鱼塘，经过一段时间，等有标记的鱼完全混合于鱼群中，再打捞200条鱼，发现其中带标记的鱼有5条，则鱼塘中估计有多少条鱼．若第三次打捞上10条，它们的质量分别为1.8，2，2.2，1.9，2.1，2.3，1.7，2，2.6，1，4千克，请估计这塘鱼的产量．

答案解析收藏纠错 + 选题
20. 某封闭的纸箱中有红色、黄色的玻璃球若干，为了估计出纸箱中红色、黄色球的数目，小亮向纸箱中放入25个白球，通过多次摸球实验后，发现摸到白球的频率为25％，摸到黄球的频率为40％，试估计出原纸箱中红球、黄球的数目．

答案解析收藏纠错 + 选题
21. 对某厂生产的直径为4cm的乒乓球进行产品质量检查，结果如下：
1. （1）计算各次检查中“优等品”的频率，填入表中；
  抽取球数n 50 100 500 1000 5000
  优等品数m 45 92 455 890 4500
  优等品频率 $\text{[math]}$
2. （2）该厂生产乒乓球优等品的概率约为多少?
答案解析收藏纠错 + 选题
22. (2019·巴中) 如图表示的是某班部分同学衣服上口袋的数目．
1. （1）从图中给出的信息得到学生衣服上口袋数目的中位数为，众数为．
2. （2）根据如图信息，在给出的图表中绘制频数条形统计图，由此估计该班学生衣服上口袋数目为 $\text{[math]}$ 的概率．
答案解析收藏纠错 + 选题
23. (2022九上·桐庐月考) 目前我市“校园手机”现象越来越受到社会关注，针对这种现象，我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法，统计整理并制作了如下的统计图：
1. （1）这次调查的家长总数为人．家长表示“不赞同”的人数为人；
2. （2）请在图①中把条形统计图补充完整；
3. （3）从这次接受调查的家长中随机抽查一个，恰好是“赞同”的家长的概率是；
4. （4）求图②中表示家长“无所谓”的扇形圆心角的度数．
答案解析收藏纠错 + 选题
24. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复.下表是活动进行中的一组统计数据：
1. （1）计算并完成表格；
2. （2）请估计：当n很大时，摸到白球的频率将会接近
3. （3）假如你摸一次，你摸到白球的概率是，摸到黑球的概率是；
4. （4）试估算口袋中黑、白两种颜色的球各有多少只?
答案解析收藏纠错 + 选题

25. (2020八上·郑州开学考) 从一副52张（没有大小王）的扑克中，每次抽出1张，然后放回洗匀再抽，在实验中得到下列表中部分数据：

实验次数	40	80	120	160	200	240	280	320	360	400
出现方块的次数	11	18		40	49	63	68	80	91	100
出现方块的频率	27.5%	22.5%	25%	25.25%	24.5%	26.25%	24.3%		25.28%	25%

（1）将数据表补充完整；
（2）从上面的图表中可以估计出现方块的概率是：.
（3）将这副扑克中的所有方块(即从方块1到方块13，共13张)取出，将它们背面朝上重新洗牌后，从中摸出一张，若摸出的这张牌的牌面数字为奇数，则甲方羸：若摸出的这张牌的牌面数字为偶数，则乙方赢，你认为这个游戏对双方是公平的吗?

答案解析收藏纠错 + 选题

26. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图.
1. （1）请估计：当n足够大时，摸到白球的频率将会稳定在(精确到0.01)，假如你摸一次，你摸到白球的概率为；
2. （2）试估算盒子里白、黑两种颜色的球各有多少个?
3. （3）在(2)条件下如果要使摸到白球的概率为 $\text{[math]}$ ，需要往盒子里再放入多少个白球?
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

初中数学浙教版九年级上学期期中复习专题5 用频率估计概率

副标题：

*注意事项：

初中数学浙教版九年级上学期期中复习专题5 用频率估计概率

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

抛掷次数	100	200	300	400	500
正面朝上的频数	53	98	156	202	244

抽取球数n	50	100	500	1000	5000
优等品数m	45	92	455	890	4500
优等品频率 $\text{[math]}$

石块的面	1	2	3	4	5
频数	17	28	15	16	24