北京市石景山区礼文中学2019-2020学年九年级上学期数学...

更新时间：2021-05-17 浏览次数：51 类型：期末考试

一、单选题

1. 为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（）

A . 12cm B . 10cm C . 8cm D . 6cm

答案解析收藏纠错 + 选题
2. (2020九上·石景山期末) 如图，AB是⊙O的直径，C是线段OB上的一点（不与点B重合），D，E是半圆上的点且CD与BE交于点F，用① $\text{[math]}$ ，②DC⊥AB，③FB=FD中的两个作为题设，余下的一个作为结论组成一个命题，则组成真命题的个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
3. (2020九上·石景山期末) 一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 在同一平面直角坐标系xOy中的图象如图所示，当 $\text{[math]}$ 时，x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·石景山期末) 某市为了解旅游人数的变化情况，收集并整理了2017年1月至2019年12月期间的月接待旅游量（单位：万人次）的数据并绘制了统计图如下：

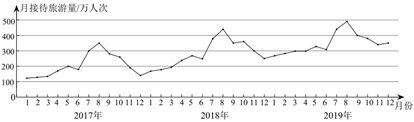
根据统计图提供的信息，下列推断不合理的是（）

A . 2017年至2019年，各年的月接待旅游量高峰期大致在7，8月份 B . 2019年的月接待旅游量的平均值超过300万人次 C . 2017年至2019年，年接待旅游量逐年增加 D . 2017年至2019年，各年下半年（7月至12月）的月接待旅游量相对于上半年（1月至6月）波动性更小，变化比较平稳

答案解析收藏纠错 + 选题
5. (2020九上·石景山期末) 如图，△ABC的顶点都在正方形网格的格点上，则cos∠BAC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·石景山期末) 如图，AB是 $\text{[math]}$ 的直径，CD是弦，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·石景山期末) 如图，某斜坡的长为100m，坡顶离水平地面的距离为50m，则这个斜坡的坡度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

8. (2020九上·石景山期末) 已知抛物线 $\text{[math]}$ 上部分点的横坐标x与纵坐标y的对应值如下表

x	…	-2	-1	0	1	2	3	…
y	…	-4	0	2	2	0	-4	…

下列结论：①抛物线开口向下；②当 $\text{[math]}$ 时，y随x的增大而减小；③抛物线的对称轴是直线 $\text{[math]}$ ；④函数 $\text{[math]}$ 的最大值为2.其中所有正确的结论为（）

A . ①②③ B . ①③ C . ①③④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题

9. (2020九上·石景山期末) 若抛物线 $\text{[math]}$ 与x轴只有一个交点，则m的值为.

答案解析收藏纠错 + 选题
10. (2020九上·石景山期末) 如图，在 $\text{[math]}$ 中，点D在AB上，点E在AC上， $\text{[math]}$ ，若 $\text{[math]}$ ，四边形DBCE的面积是 $\text{[math]}$ 的面积的3倍，则BC的长为.

答案解析收藏纠错 + 选题
11. (2020九上·石景山期末) 如图，等边 $\text{[math]}$ 内接于 $\text{[math]}$ ，若 $\text{[math]}$ 的半径为3，则阴影部分的面积为.

答案解析收藏纠错 + 选题
12. (2020九上·石景山期末) 如图，在矩形ABCD中，点E是边AD上一点， $\text{[math]}$ 于点F.若 $\text{[math]}$ ， $\text{[math]}$ ，则AE的长为.

答案解析收藏纠错 + 选题
13. (2020九上·昌平期末) 请写出一个开口向上，并且与y轴交于点（0，-2）的抛物线的表达式．

答案解析收藏纠错 + 选题
14. (2020九上·石景山期末) 将抛物线 $\text{[math]}$ 向左平移1个单位长度，所得抛物线的表达式为.

答案解析收藏纠错 + 选题
15. (2020九上·石景山期末) 《九章算术》是中国传统数学重要的著作之一，奠定了中国传统数学的基本框架.其中卷九中记载了一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”其意思是：“如图，今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆（内切圆）的直径是多少步？”根据题意，该内切圆的直径为步.

答案解析收藏纠错 + 选题
16. (2020九上·石景山期末) 如图，曲线AB是抛物线 $\text{[math]}$ 的一部分（其中A是抛物线与y轴的交点，B是顶点），曲线BC是双曲线 $\text{[math]}$ 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点 $\text{[math]}$ ， $\text{[math]}$ 在该“波浪线”上，则m的值为，n的最大值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2020九上·石景山期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2020九上·石景山期末) 在平面直角坐标系xOy中，二次函数 $\text{[math]}$ 的图象与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，顶点为P.
1. （1）直接写出点A，C，P的坐标.
2. （2）画出这个函数的图象.
答案解析收藏纠错 + 选题
19. (2020九上·石景山期末) 下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.

已知：如图1， $\text{[math]}$ 及 $\text{[math]}$ 上一点P.

求作：直线PQ，使得PQ与 $\text{[math]}$ 相切.

作法：如图2，

①连接PO并延长交 $\text{[math]}$ 于点A；

②在 $\text{[math]}$ 上任取一点B（点P，A除外），以点B为圆心，BP长为半径作 $\text{[math]}$ ，与射线PO的另一个交点为C.

③连接CB并延长交 $\text{[math]}$ 于点Q.

④作直线PQ；

所以直线PQ就是所求作的直线.

根据小石设计的尺规作图的过程.
1. （1）使用直尺和圆规，补全图形：（保留作图痕迹）
2. （2）完成下面的证明.
  证明：∵CQ是的 $\text{[math]}$ 直径，
  
  ∴ $\text{[math]}$ $\text{[math]}$ （）（填推理的依据）
  
  ∴ $\text{[math]}$ .
  
  又∵OP是 $\text{[math]}$ 的半径，
  
  ∴PQ是 $\text{[math]}$ 的切线（）（填推理的依据）
答案解析收藏纠错 + 选题
20. (2021九上·合肥月考) 为了在校运会中取得更好的成绩，小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是 $\text{[math]}$ 米，当铅球运行的水平距离为3米时，达到最大高度 $\text{[math]}$ 的B处.小丁此次投掷的成绩是多少米？

答案解析收藏纠错 + 选题
21. (2020九上·石景山期末) 在直角三角形中，除直角外的5个元素中，已知2个元素（其中至少有1个是边），就可以求出其余的3个未知元素.对于任意三角形，我们需要知道几个元素就可以求出其余的未知元素呢？思考并解答下列问题：
1. （1）观察图①~图④，根据图中三角形的已知元素，可以求出其余未知元素的序号是.
2. （2）如图⑤，在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，能否求出BC的长度？如果能，请求出BC的长度；如果不能，请说明理由.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
22. (2020九上·石景山期末) 在平面直角坐标系xOy中，函数 $\text{[math]}$ 的图象G经过点 $\text{[math]}$ ，直线 $\text{[math]}$ 与y轴交于点B，与图象G交于点C．
1. （1）求m的值.
2. （2）横、纵坐标都是整数的点叫做整点.记图象G在点A，C之间的部分与线段BA，BC围成的区域（不含边界）为W.
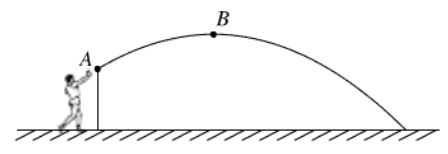
  ①当直线l过点 $\text{[math]}$ 时，直接写出区域W内的整点个数.
  
  ②若区域W内的整点不少于4个，结合函数图象，求k的取值范围.
答案解析收藏纠错 + 选题
23. (2020九上·石景山期末) 如图，B是 $\text{[math]}$ 的半径OA上的一点（不与端点重合），过点B作OA的垂线交 $\text{[math]}$ 于点C，D，连接OD，E是 $\text{[math]}$ 上一点， $\text{[math]}$ ，过点C作 $\text{[math]}$ 的切线l，连接OE并延长交直线l于点F.
1. （1） ①依题意补全图形.
  ②求证：∠OFC=∠ODC．
2. （2）连接FB，若B是OA的中点， $\text{[math]}$ 的半径是4，求FB的长.
答案解析收藏纠错 + 选题

24. (2020九上·石景山期末) 某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查，分别随机抽取了 50 件产品并对某一项关键质量指标做检测，获得了它们的质量指标值 s ，并对样本数据（质量指标值 s ）进行了整理、描述和分析．下面给出了部分信息．

a ．该质量指标值对应的产品等级如下：

质量指标值	20 ≤ s < 25	25 ≤ s < 30	30 ≤ s < 35	35 ≤ s < 40	40 ≤ s ≤ 45
等级	次品	二等品	一等品	二等品	次品

说明：等级是一等品，二等品为质量合格(其中等级是一等品为质量优秀)；等级是次品为质量不合格．

b ．甲企业样本数据的频数分布统计表如下（不完整）：

c ．乙企业样本数据的频数分布直方图如下：

d ．两企业样本数据的平均数、中位数、众数、方差如下：

	平均数	中位数	众数	方差
甲企业	31.92	32.5	34	11.87
乙企业	31.92	31.5	31	15.34

根据以上信息，回答下列问题：

（1） m 的值为， n 的值为；
（2）若从甲企业生产的产品中任取一件，估计该产品质量合格的概率为；若乙企业生产的某批产品共5 万件，估计质量优秀的有万件；
（3）根据图表数据，你认为企业生产的产品质量较好，理由为．（从某个角度说明推断的合理性）

答案解析收藏纠错 + 选题

25. (2020九上·石景山期末) 如图，C是 $\text{[math]}$ 的一定点，D是弦AB上的一定点，P是弦CB上的一动点.连接DP，将线段PD绕点P顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ .射线 $\text{[math]}$ 与 $\text{[math]}$ 交于点Q.已知 $\text{[math]}$ ，设P，C两点间的距离为xcm，P，D两点间的距离 $\text{[math]}$ ，P，Q两点的距离为 $\text{[math]}$ .

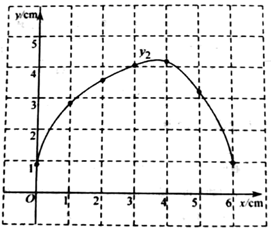
小石根据学习函数的经验，分别对函数 $\text{[math]}$ ， $\text{[math]}$ ，随自变量x的变化而变化的规律进行了探究，下面是小石的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了 $\text{[math]}$ ， $\text{[math]}$ ，与x的几组对应值：

x/cm	0	1	2	3	4	5	6
$\text{[math]}$ /cm	4.29	3.33		1.65	1.22	1.50	2.24
$\text{[math]}$ /cm	0.88	2.84	3.57	4.04	4.17	3.20	0.98

（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数据所对应的点 $\text{[math]}$ ， $\text{[math]}$ ，并画出函数 $\text{[math]}$ ， $\text{[math]}$ 的图象；
（3）结合函数图象，解决问题：连接DQ，当△DPQ为等腰三角形时，PC的长度约为cm.（结果保留一位小数）

答案解析收藏纠错 + 选题

26. (2020九上·石景山期末) 在平面直角坐标系xOy中，抛物线y=ax²-4ax+c(a≠0)与y轴交于点A，将点A向右平移2个单位长度，得到点B．直线 $\text{[math]}$ 与x轴，y轴分别交于点C，D．
1. （1）求抛物线的对称轴.
2. （2）若点A与点D关于x轴对称.
  ①求点B的坐标.
  
  ②若抛物线与线段BC恰有一个公共点，结合函数图象，求a的取值范围.
答案解析收藏纠错 + 选题
27. (2021九上·顺义月考) 如图，在正方形ABCD中，P是边BC上的一动点（不与点B，C重合），点B关于直线AP的对称点为E，连接AE，连接DE并延长交射线AP于点F，连接BF
1. （1）若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的大小（用含 $\text{[math]}$ 的式子表示）.
2. （2）求证： $\text{[math]}$ .
3. （3）连接CF，用等式表示线段AF，BF，CF之间的数量关系，并证明.
答案解析收藏纠错 + 选题
28. (2020九上·石景山期末) 在 $\text{[math]}$ 中，D是边BC上一点，以点A为圆心，AD长为半径作弧，如果与边BC有交点E（不与点D重合），那么称 $\text{[math]}$ 为 $\text{[math]}$ 的A-外截弧.例如，图中 $\text{[math]}$ 是 $\text{[math]}$ 的一条A-外截弧.在平面直角坐标系xOy中，已知 $\text{[math]}$ 存在A-外截弧，其中点A的坐标为 $\text{[math]}$ ，点B与坐标原点O重合.
1. （1）在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，满足条件的点C是.
2. （2）若点C在直线 $\text{[math]}$ 上.
  ①求点C的纵坐标的取值范围.
  
  ②直接写出 $\text{[math]}$ 的A-外截弧所在圆的半径r的取值范围.
答案解析收藏纠错 + 选题