浙江省宁波市慈溪市2020届九年级上学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：356 类型：期末考试

一、单选题

1. (2020九上·慈溪期末) 如图，从左边的等边三角形到右边的等边三角形，经过下列一次变化不能得到的是(　　)

A . 轴对称 B . 平移 C . 绕某点旋转 D . 先平移再轴对称

答案解析收藏纠错 + 选题
2. (2020九上·慈溪期末) 如图所示，若△ABC∽△DEF，则∠E的度数为（）

A . 28° B . 32° C . 42° D . 52°

答案解析收藏纠错 + 选题
3. (2020九上·慈溪期末) 下列事件中是随机事件的是(　　)

A . 校运会上立定跳远成绩为10米 B . 在只装有5个红球的袋中，摸出一个红球 C . 慈溪市明年五一节是晴天 D . 在标准大气压下，气温3℃ 时，冰熔化为水

答案解析收藏纠错 + 选题
4. (2021九上·思明期中) 如图，⊙O中，点D，A分别在劣弧BC和优弧BC上，∠BDC=130°，则∠BOC=(　　)

A . 120° B . 110° C . 105° D . 100°

答案解析收藏纠错 + 选题
5. (2020九上·慈溪期末) 在Rt△ABC中，∠C=90°，AB=5，AC=3，则下列等式正确的是(　　)

A . sinA= $\text{[math]}$ B . cosA= $\text{[math]}$ C . tanA= $\text{[math]}$ D . cosA= $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·商河期末) 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

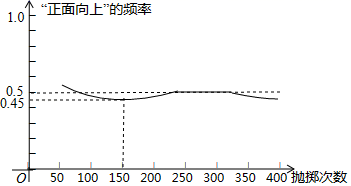
下面有三个推断：

①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；

②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；

③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．

其中合理的是（　　）

A . ① B . ② C . ①② D . ①③

答案解析收藏纠错 + 选题
7. (2020九上·慈溪期末) 下列命题是真命题的是(　　)

A . 在同圆或等圆中，等弧所对的圆周角相等 B . 平分弦的直径垂直于弦 C . 在同圆或等圆中，等弦所对的圆周角相等 D . 三角形外心是三条角平分线的交点

答案解析收藏纠错 + 选题
8. (2024九上·分宜期中) 在平面直角坐标系中，把抛物线y=2x²绕原点旋转180°，再向右平移1个单位，向下平移2个单位，所得的抛物线的函数表达式为(　　)

A . y=2(x﹣1)²﹣2 B . y=2(x+1)²﹣2 C . y=﹣2(x﹣1)²﹣2 D . y=﹣2(x+1)²﹣2

答案解析收藏纠错 + 选题
9. (2020九上·慈溪期末) 如图，在△ABC中，D，E，F分别为BC，AB，AC上的点，且EF∥BC，FD∥AB，则下列各式正确的是(　　)

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·慈溪期末) 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知 $\text{[math]}$ ，则球的半径长是（）

A . 2 B . 2.5 C . 3 D . 4

答案解析收藏纠错 + 选题
11. (2024九下·大荔模拟) 已知，当﹣1≤x≤2时，二次函数y=m(x﹣1)²﹣5m+1(m≠0，m为常数)有最小值6，则m的值为(　　)

A . ﹣5 B . ﹣1 C . ﹣1.25 D . 1

答案解析收藏纠错 + 选题
12. (2021九上·大渡口期末) 如图，已知，M，N分别为锐角∠AOB的边OA，OB上的点，ON=6，把△OMN沿MN折叠，点O落在点C处，MC与OB交于点P，若MN=MP=5，则PN=（）

A . 2 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2020九上·慈溪期末) 写出一个图象的顶点在原点，开口向下的二次函数的表达式.

答案解析收藏纠错 + 选题
14. (2024九上·徐汇期中) 若两个相似三角形的周长比为2：3，则它们的面积比是．

答案解析收藏纠错 + 选题
15. (2020九上·慈溪期末) 已知，⊙O的半径为6，若它的内接正n边形的边长为6 $\text{[math]}$ ，则n=.

答案解析收藏纠错 + 选题
16. (2021·湖南模拟) 如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，则大厅两层之间的高度为米．（结果保留两个有效数字）（参考数据；sin31°=0.515，cos31°=0.857，tan31°=0.601）

答案解析收藏纠错 + 选题
17. (2020九上·慈溪期末) 如图，⊙O过正方形网格中的格点A，B，C，D，点E也为格点，连结BE交⊙O于点F，P为 $\text{[math]}$ 上的任一点，则tanP=.

答案解析收藏纠错 + 选题
18. (2020九上·慈溪期末) 若二次函数的图象与x轴的两个交点和顶点构成等边三角形，则称这样的二次函数的图象为标准抛物线.如图，自左至右的一组二次函数的图象T₁ ， T₂ ， T₃……是标准抛物线，且顶点都在直线y= $\text{[math]}$ x上，T₁与x轴交于点A₁(2，0)，A₂(A₂在A₁右侧)，T₂与x轴交于点A₂ ， A₃ ， T₃与x轴交于点A₃ ， A₄ ， ……，则抛物线T_n的函数表达式为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020九上·慈溪期末) 解下列两题：
1. （1）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）已知α为锐角，且2 $\text{[math]}$ sinα=4cos30°﹣tan60°，求α的度数.
答案解析收藏纠错 + 选题
20. (2020九上·慈溪期末) 如图，转盘A中的4个扇形的面积相等，转盘B中的3个扇形面积相等.小明设计了如下游戏规则：甲、乙两人分别任意转动转盘A、B一次，当转盘停止转动时，将指针所落扇形中的2个数相乘，如果所得的积是偶数，那么是甲获胜；如果所得的积是奇数，那么是乙获胜.这样的规则公平吗？为什么？

答案解析收藏纠错 + 选题
21. (2020九上·慈溪期末) 如图是四个全等的小矩形组成的图形，这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
1. （1）若每个小矩形的较短边长为1，则BC=；
2. （2） ①在图1、图2中分别画一个格点三角形(顶点是格点的三角形)，使它们都与△ABC相似(但不全等)，且图1，2中所画三角形也不全等).
  ②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹，点M用黑点表示，并注上字母M)
答案解析收藏纠错 + 选题
22. (2020九上·慈溪期末) 如图，二次函数y=ax²+bx+c过点A(﹣1，0)，B(3，0)和点C(4，5).
1. （1）求该二次函数的表达式及最小值.
2. （2）点P(m，n)是该二次函数图象上一点.
  ①当m=﹣4时，求n的值；
  
  ②已知点P到y轴的距离不大于4，请根据图象直接写出n的取值范围.
答案解析收藏纠错 + 选题
23. (2021·诸暨模拟) 如图1，是一种自卸货车.如图2是货箱的示意图，货箱是一个底边AB水平的矩形，AB=8米，BC=2米，前端档板高DE=0.5米，底边AB离地面的距离为1.3米.卸货时，货箱底边AB的仰角α=37°(如图3)，求此时档板最高点E离地面的高度.(精确到0.1米，参考值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)

答案解析收藏纠错 + 选题
24. (2021九上·大余期末) 某商品市场销售抢手，其进价为每件80元，售价为每件130元，每个月可卖出500件；据市场调查，若每件商品的售价每上涨1元，则每个月少卖2件(每件售价不能高于240元).设每件商品的售价上涨x元(x为正整数)，每个月的销售利润为y元.
1. （1）求y与x的函数关系式，并直接写出自变量x的取值范围；
2. （2）每件商品的涨价多少元时，每个月可获得最大利润？最大的月利润是多少元？
3. （3）每件商品的涨价多少元时，每个月的利润恰为40000元？根据以上结论，请你直接写出x在什么范围时，每个月的利润不低于40000元？
答案解析收藏纠错 + 选题
25. (2020九上·慈溪期末) 定义：连结菱形的一边中点与对边的两端点的线段把它分成三个三角形，如果其中有两个三角形相似，那么称这样的菱形为自相似菱形.
1. （1）判断下列命题是真命题，还是假命题？
  ①正方形是自相似菱形；
  
  ②有一个内角为60°的菱形是自相似菱形.
  
  ③如图1，若菱形ABCD是自相似菱形，∠ABC=α(0°＜α＜90°)，E为BC中点，则在△ABE，△AED，△EDC中，相似的三角形只有△ABE与△AED.
2. （2）如图2，菱形ABCD是自相似菱形，∠ABC是锐角，边长为4，E为BC中点.
  ①求AE，DE的长；
  
  ②AC，BD交于点O，求tan∠DBC的值.
答案解析收藏纠错 + 选题
26. (2020九上·慈溪期末) 如图，AB是半圆O的直径，C为半圆弧上一点，在AC上取一点D，使BC=CD，连结BD并延长交⊙O于E，连结AE，OE交AC于F.
1. （1）求证：△AED是等腰直角三角形；
2. （2）如图1，已知⊙O的半径为 $\text{[math]}$ .
  ①求 $\text{[math]}$ 的长；
  
  ②若D为EB中点，求BC的长.
3. （3）如图2，若AF：FD=7：3，且BC=4，求⊙O的半径.
答案解析收藏纠错 + 选题