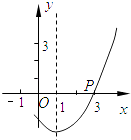

 B .
B .  C .
C .  D .
D . 
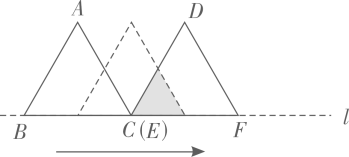
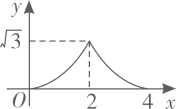 B .
B . 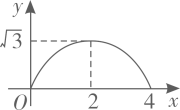 C .
C . 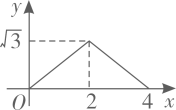 D .
D . 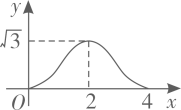

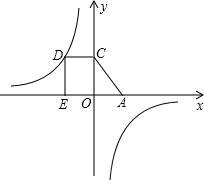

|
x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
10 |
5 |
2 |
1 |
2 |
5 |
… |

①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?