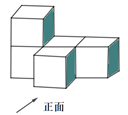
 B .
B .  C .
C .  D .
D . 

|
劳动时间(小时) |
0.5 |
1 |
1.5 |
2 |
|
人数 |
10 |
12 |
6 |
2 |
则这些学生每天劳动时间的众数是小时.
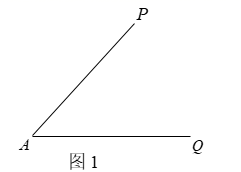
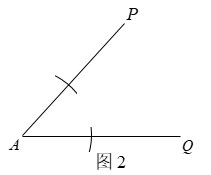
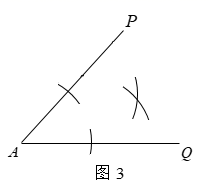
⑴如图2,以点A为圆心,任意长为半径画弧,分别与 ,
交于B,C两点;
⑵如图3,分别以B,C两点为圆心,以大于 的长为半径画弧,两弧交于点D;
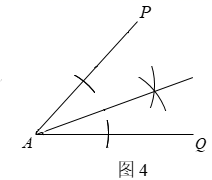
⑶如图4,作射线 ,连接
,与
交于点E.
问题:

抽取的员工竞赛成绩分布表
| 组别 | 分数/分 | 频数 |
| A | | |
| B | | 12 |
| C | | 6 |
| D | | 3 |
扇形统计图
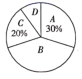
B组的成绩分别是88,86,80,86,84,82,80,86,82,84,88,86.(单位:分)
请解答下列问题:

|
课题 |
测量山上塔的高度 |
||||
|
测量工具 |
测量角度的仪器,皮尺等 |
||||
|
测量示意图 |
|
说明:线段 CD 表示山高, CB 表示塔的高,测量角度的仪器的高度 |
|||
|
测量数据 |
测量项目 |
第一次 |
第二次 |
第三次 |
平均值 |
|
|
63.6° |
63.3° |
63.3° |
63.4° |
|
|
|
29.9° |
29.8° |
30.3° |
30° |
|
|
|
44.9° |
45.3° |
44.8° |
__________ |
|
|
A,E之间的距离 |
50.1m |
49.8m |
50.1m |
__________ |
|
|
… |
… |
||||
(结果精确到0.1m.参考数据: ,
,
,
,
)
公元前5世纪,古希腊学者提出了一个问题:能否用尺规三等分一个任意角?为了解决这个问题,数学家们花费了大量的时间和精力.直到1837年,数学家们才证明了“三等分任意角”是不能用尺规完成的.那么.退而求其次,能不能借助一些特殊曲线解决这一问题呢?
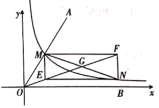
在研究这个问题的过程中,古希腊数学家帕普斯给出的一方法如下:如图,将给定的锐角 置于平面直角坐标系中,角的一边
与
的图象交于点M,
在
轴上,以点M为圆心,
为半径画弧交
的图象于点N.分别过点M和N作
轴和
轴的平行线,两线相交于点E,F,
和
相交于点G,连接
得到
.
此时,爱思考的小明对这一结论展开了证明.下面是他的部分证明思路:
由题意,可知点M,N在反比例函数 的图象上,
先假设点M,N的坐标分别为 ,
,
则点E,F的坐标可表示为 ,
则直线 的表达式为__.
由此,可以判断矩形 的顶点E在直线
上.
…
请根据以上材料,解答下列问题:
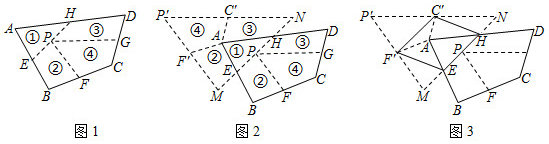
关于在拼接过程中用到的图形的变换,说法正确的是( )
①当点E在第一象限,且 时,求
的值.
②若D,E,P三个点中恰有一点是其他两点所连线段的中点(三点重合除外),则称D,E,P三点为“共生点”.当点D,E,P三点为“共生点”时,请直接写出 的值.